邊際生產力

邊際生產力理論有兩要素形式和多要素形式來說明生產要素的需求量。兩要素是指總資本和總勞動，在這種形式下，生產函數的形式是Y=F(L,K)，L、K分別是生產過程中投入的勞動和資本的數量。多要素是指在生產過程中使用的可分辨要素的種類，就是在本文開始部分所採用的那種形式。兩要素形式可以使邊際生產力理論進行簡化，但是這個模型存在著一個致命的弱點，就是如何將一個廠商投入的不同質的勞動和不同質的資本進行加總，（註：加總問題是邊際生產力理論所遇到的最大的困難，邊際生產力需要一個總量勞動和資本的概念，資本的加總只能通過對其價值（格）進行加總的形式來實現，而資本的價格受到資本的邊際生產力（利息率）的影響，即維克賽爾效應，從而使邊際生產力理論成為一個循環論證。）這也是在上個世紀劍橋資本爭論最為激烈的一個問題。多要素形式避免了對不同的勞動和資本進行加總，但這種形式卻遠離現實，因為這種形式會使生產函數連續可微分的性質難以成立：許多廠商的投入要素都是固定比例，不可能單獨地增減一種生產要素而不增減其他的生產要素，即生產要素之間不存在替代性，這樣沒有辦法得出一種要素的邊際生產力，因此邊際生產力的理論適用範圍非常有限。本文在這裡分析的是邊際生產力理論的適用範圍，因此，在這裡採用的是兩要素生產模型，將廠商的投入抽象地分為勞動和資本，而如何將異質的資本和勞動加總的問題給拋開，而抽象地認為勞動和資本是同質的。

規模報酬遞增是現代化生產中必然存在的現象，那麼邊際生產力理論必然要對這種與其相矛盾的規模報酬遞增給以解釋。

一種解釋認為經濟中不存在規模報酬遞增的現象，之所以產生規模報酬遞增，是由於有一種促使規模報酬遞增的生產要素被人們忽視了，只要加入新的生產要素，生產函數就不會存在規模遞增現象：兩種要素的生產函數解釋不了現實經濟的真實情況，在現代經濟中，生產要素也在多元化，科學技術、知識、教育等因素加入到生產函數中去，生產函數成了Y=F(L,K,T,I,E……)，從而使生產函數變得越來越複雜，這樣處理之後，生產函數就成為線性齊次性，就可以滿足於總額相符，從而就使邊際生產力學說更加完美，甚至進一步找出科技、知識、教育等在生產過程中的作用來。這種學說存在著一個明顯的錯誤，根據生產要素的性質，生產要素起著兩個方面的作用，一是生產過程的投入物，二是要在生產過程中得到相應的報酬。儘管我們可以通過複雜的計算得出科技、知識和教育的邊際生產力，但是是誰根據這些要素的邊際生產力而得到它的報酬呢？是工人，還是資本家，還是科學家？另外，科技和知識都是體現在勞動和資本中，不能從勞動和資本中獨立出來，生產函數的形式應該是Y=F[L(T,I,E……),K(T,I,E……)]，這樣，從數學的邏輯上分析，自變數之間必然是獨立的，即有完全的自由度。如果技術、知識、教育和勞動、資本之間存在著相關性，它們就不可能同時作為生產函數的自變數，即同時成為生產要素。因此，用多生產要素的生產函數使之成為線性齊次性，從而可以使之滿足總額相符的方法，是存在著邏輯矛盾。

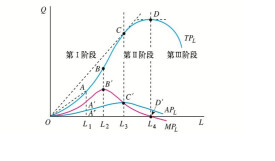
還有一種解釋的方法是採用改變生產函數的方法，認為生產函數是不斷變動，即將生產函數動態化而成為Y=F[,t](L,K)。認為在靜態中，不存在著規模報酬遞增，只存在著規模報酬不變的現象，之所以存在規模報酬是因為隨著時間的變化，生產函數發生了變動，而這種變動的主要原因還是歸因於技術進步導致了生產函數的移動。在這裡，我們用數學的形式加以說明：在靜態中，生產函數的形式是Y=F(L,K)，由於是規模報酬不變，即存在線性齊次性，因此可以得到：Y/L=F(L,K)/L=F(1,K/L)，Y/L是單位勞動的產出，即勞動生產率，我們用y來表示，K/L是資本勞動比，我們用k來表示，那麼，生產函數就可以表示成y=F(1,k)，我們用一個新函數f(k)來代表F(1,k)，那麼就得出線性齊次生產函數可以表示為這樣的形式：勞動生產率是資本勞動比的一個函數，一般情況，這個函數是凸性，即f′(k)>0,f″(k)<0（如圖中的f[,1](k)）。隨著時間的改變，技術進步改變了生產函數的位置，生產函數從時間t[,1]的f(,1)(k)移動到t[,2]的f[,2](k)。這樣在每個靜態的時點上，生產函數是線性齊次性，因此可以滿足總額相等原理，從而生產要素可以按照邊際生產力得到相應的報酬。而在不同時間上，這種生產函數的移動體現的是技術進步對生產過程的影響。變動的生產函數不利於數學分析，因此把生產函數Y=F[,1](L,K)變形為Y=F(L,K,t)，t代表著時間。進一步，新古典理論又把生產函數擴展到宏觀總量生產函數，因素t不包括來自增加資本和勞動投入的貢獻，為技術進步的貢獻，是扣除勞動和資本增加投入的影響后剩下的部分。很明顯，這樣的處理方法和前一種方法是相同的，只不過是把技術、知識和教育等因素全部歸因於時間的變動。