正整數
大於0的整數
和整徠數一樣,正整數也是一個可數的無限集合。在數論中,正整數,即1、2、3;但在集合論和計算機科學中,自然數則通常是指非負整數,即正整數與0的集合,也可以說成是除了0以外的自然數就是正整數。正整數又可分為質數,1和合數。正整數可帶正號(+),也可以不帶。

正整數
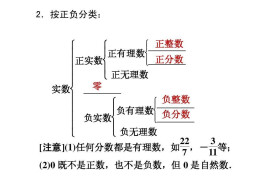
我們以0為界限,將整數分為三大類:
1.正整數,即大於0的整數,如,1,2,3…
2.0既不是正整數,也不是負整數(0是整數)。
3.負整數,即小於0的整數,如,-1,-2,-3…
我們知道正整數的一種分類辦法是按照其約數或積因子的多少來劃分的,比如僅僅有兩個的(當然我們總是多餘地強調這兩個是1和其本身),我們就稱之為質數或素數,而多於兩個的就稱之為合數。
利用皮亞諾公理可以對正整數及N*進行如下描述:
任何一個滿足下列條件的非空集合叫做正整數集合,記作N*。如果
Ⅰ1是正整數;
Ⅱ每一個確定的正整數a,都有一個確定的後繼數a',a'也是正整數(數a的後繼數a‘就是緊接在這個數後面的整數(a+1)。例如,1‘=2,2’=3等等。);
Ⅲ如果b、c都是正整數a的後繼數,那麼b=c;
Ⅳ1不是任何正整數的後繼數;
Ⅴ設S⊆N*,且滿足2個條件(i)1∈S;(ii)如果n∈S,那麼n'∈S。那麼S是全體正整數的集合,即S=N*。(這條公理也叫歸納公理,保證了數學歸納法的正確性)
皮亞諾公理對N*進行了刻畫和約定,由它們可以推出關於正整數的各種性質。
正整數的唯一分解定理:又稱為算術基本定理。
即:每個大於1的自然數均可寫為若干個質數的冪的積,而且這些素因子按大小排列之後,寫法是唯一的。
若X,N∈N*,則X>N等價於X≥N+1。
關於正整數的六邊形數部分
對任意正數n,設b(n)表示n的最大六邊形數部分,即就是b(n)=m(2m-1),如果m(2m-1)≤n<(m+1)(2m+1),m∈N。
前n個正整數的k次方的組合表示
用若干個形如的展開形式求