穩態誤差
系統受擾動重新平衡產生的偏差
穩態誤差是系統從一個穩態過度到新的穩態,或系統受擾動作用又重新平衡后,系統出現的偏差。穩態誤差記作ess(Steady-State Errors)。
穩態誤差
穩態誤差類穩態誤差按照產誤差際誤差類。
①誤差跟蹤輸量值擾存,控制系統必存類穩態誤差。穩態誤差零,控制系統稱靜差系統,否則稱靜差系統。穩態誤差否消除,取決系統組否包含積環節(控制系統典型環節)。
②實際性誤差系統的組成部件中的不完善因素(如摩擦、間隙、不靈敏區等)所造成的穩態誤差。這種誤差是不可能完全消除的,只能通過選用高精度的部件,提高系統的增益值等途徑減小。
穩態誤差按照產生的原因分為原理性誤差和實際性誤差兩類。
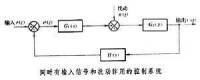
通常,伺服系統為無靜差系統,而自動調節系統為有靜差系統。對於無靜差系統,無靜差性是相對於某種特定形式的輸入信號或擾動作用而言的。一個控制系統對於單位階躍函數(見拉普拉斯變換)的輸入信號或擾動作用是無靜差的,並不表示它對單位斜坡函數的輸入或擾擾動也是無靜差的。對於同時有輸入r(t)和擾動n(t)作用的控制系統(見圖),在系統為漸近穩定(見穩定性)的前提下,原理性誤差ess規定為t→∞時控制誤差e(t)的值。ess由兩部分組成,一部分是由輸入信號引起的穩態誤差esr,另一部分是由擾動作用引起的穩態誤差esn,即ess=esr+esn。用G1(s)、G2(s)、H(s)分別表示系統各部分的傳遞函數,並令G(s)=G1(s)G2(s)為系統前饋通道的傳遞函數,則系統穩態誤差與系統傳遞函數間的關係為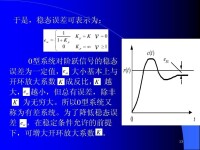

穩態誤差
其中R(s)和N(s)分別是輸入r(t)和擾動n(t)的拉普拉斯變換,s為複數自變數。
系統的組成部件中的不完善因素(如摩擦、間隙、不靈敏區等)所造成的穩態誤差。
系統的結構類型 在控制系統的研究中,常常按系統組成中所包含的積分環節的個數對系統進行分類,這對研究不同典型輸入作用下系統的穩態誤差是很方便的。系統前饋通道中不包含積分環節時稱為0型系統,包含一個積分環節時稱為Ⅰ型系統,包含兩個積分環節時稱為Ⅱ型系統。高於Ⅱ型的系統一般沒有實際意義,這種結構的控制系統很難具有滿意的過渡過程性能,在工程上幾乎不採用。表1為各型控制系統在三種典型輸入信號(單位階躍函數1(t)、單位斜坡函數t、單位加速度函數t2)作用下的穩態誤差ess,其中K 表示系統的開環增益。
靜態誤差係數 在控制系統的分析中,通常採用靜態誤差係數作為衡量系統穩態性能的一種品質指標,靜態誤差係數能表徵系統所具有的減小或消除穩態誤差的能力。靜態誤差係數越大,系統的穩態誤差就越小;當靜態誤差係數為∞時,系統沒有穩態誤差。靜態誤差係數包括位置誤差係數Kp、速度誤差係數Kv、加速度誤差係數Ka。
用G(s)H(s)表示控制系統的開環傳遞函數,則三種誤差係數與G(s)H(s)的關係為
$$ Kp=【G(s)H(s)】S=0
Kv=【sG(s)H(s)】S=0
Ka=【s^2G(s)H(s)】S=0!! 表2為各型控制系統的靜態誤差係數值。表3為三種典型輸入信號作用下系統穩態誤差和靜態誤差係數間的關係,其中K 為系統的開環增益。
