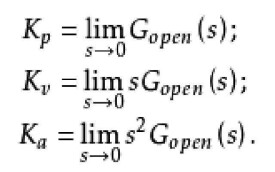靜態誤差係數
控制系統領域中計算的係數
設系統框圖圖示,析靜態誤差系統傳遞函系,且,采圖()誤差。
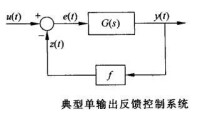
圖1
式 是閉環系統的開環傳遞函數。
如果e(t)是有終值的,根據拉普拉斯變換的終值定理有
可以看出,對於給定的輸入量 關於輸入量的靜態誤差 只取決於系統的開環傳遞函數。
當輸人信號為三種典型信號之一時,上式化為
對於單位階躍函數
對於單位斜坡函數
對於單位加速度函數
定義靜態誤差係數如下:
位置誤差係數:
速度誤差係數:
加速度誤差係數:
把式(4)、(5)、(6)分別代人式(1)、(2)、(3)中,得
對於單位階躍函數:
對於單位斜坡函數:
對於單位加速度函數:
通常有,於是式(7)化為,與另外兩個公式形式上相似。這表明:採用靜態誤差係數概念后可以認為,系統在三種典型輸入信號作用下的 靜態誤差等於或近似等於相應的誤差係數的倒數。
與系統的結構和參數的關係
下面進一步考察靜態誤差係數與系統的結構和參數的關係。
將系統的開環傳遞函數一般地寫成
的形式,式中K是系統的開環比例係數;各 和各 都可以是實數或共軛複數 分母中的因子 表明開環傳遞函數中含有 個積分單元,工程上按照v的值分別稱系統為0型,1型,2型,的系統實際上極少遇到,因為 含有多於兩個積分單元的系統很難使之穩定,因此一般情形下只使用0型,1型和2型的系統。
把式(10)代人靜態誤差係數的定義式(4)、(5)、(6)中得
從上式分別求出各型系統的靜態誤差係數,列於表1;再從式(7)、(8)、(9)分別求出靜態誤差,列於表2。從這兩個表可以看出:首先,就同一典型輸入信號而言,積分單元數目愈多的系統,靜態誤差愈小;而就同一系統而言,輸入信號變化率愈大,靜態誤差愈大。其次,不含積分單元的0型系統在階躍輸入信號下必有靜差,所以稱作 有靜差系統,對於有靜差系統,只要在保證系統穩定的前提下提高系統的開環比例係數,就可以減小靜差,至於含有積分單元的1型和2型系統,它們在階躍輸入信號作用下沒有靜差,稱作 無靜差系統,有 個積分單元就稱為 階的無靜差系統,或說系統的 無靜差度是。
| 表1 各型系統的靜態誤差係數 | |||
|---|---|---|---|
| 系統類型 | 位置誤差係數 | 速度誤差係數 | 加速度誤差係數 |
| 0型() | K | ||
| 1型() | K | ||
| 2型() | K | ||
| 表2 各型系統的靜態誤差 | |||
|---|---|---|---|
| 系統類型 | 單位階躍函數輸入 | 單位斜坡函數輸人 | 單位加速度函數輸入 |
| 0型() | |||
| 1型() | |||
| 2型() | |||
顯然,用0型系統跟蹤恆速變化的信號時,它的輸出量的速度總是趕不上輸入信號的速度,以致差距愈來愈大,1型系統則能以同樣速度跟蹤恆速變化的信號,但有一定的靜差,以致輸出量總比輸入信號“落後”一個固定的量,輸入信號變化的速度愈大,落後的量也愈大,圖2表示單位反饋的1型系統對斜坡輸入信號的響應。
從表2還可以看出,0型和1型系統都不能跟蹤恆加速度信號,而2型系統能跟蹤恆加速度信號,但有靜態誤差,換句話說,它的輸出量能與輸入信號以同一加速度和同一速度變化,但總是“落後”一個固定的量。圖3表示單位反饋的2型系統對恆加速度輸入信號的響應。
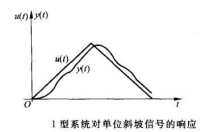
圖2
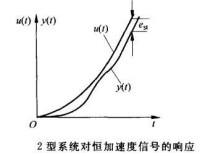
圖3
綜上所述,在保證系統穩定的前提下,如果系統的前向通道中積分單元數目愈多,則愈可以提高系統的無靜差度,例如在0型系統的主通道中增加一個積分單元,就變成1型系統,對階躍輸入信號就由原來的有靜差變成無靜差。另外,增大系統的開環比例係數可以減小靜態誤差,這為選擇系統的開環比例係數提供了依據。例如,要求某0型系統的靜態誤差不超過1%,則至少應選K為99;如果要求1型系統在信號變化速度為1°/s時的靜態跟蹤誤差不超過1',則至少應選K為60s。