艾佛森括弧
艾佛森括弧
在數學中,以Kenneth E. Iverson命名的“艾佛森括弧”,是一種用方括弧記號,如果方括弧內的條件滿足則為1,不滿足則為0。
該記號由Kenneth E. Iverson在他的編程語言APL中引進,而特別使用方括弧則是由高德納倡導的,目的是避免含括弧的表達式中的歧義。
艾佛森括弧
艾佛森括弧
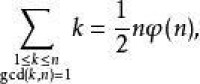
艾佛森括弧
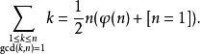
艾佛森括弧
艾佛森括弧
符號函數和單位階躍函數:
艾佛森括弧
艾佛森括弧
最值與絕對值:
艾佛森括弧
艾佛森括弧
艾佛森括弧
上下取整函數:
艾佛森括弧
艾佛森括弧
麥考利括弧可被表示為
艾佛森括弧
艾佛森括弧
• 麥考利括弧