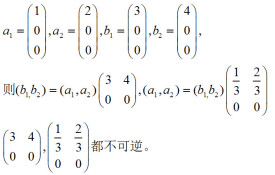等價矩陣

a1，a2，....an，線性無關，而a1，a2，....an，b，r線性相關，所以有x1a1+x2a2+....xnan+xb+yr=0，若y=0，則x1a1+x2a2+....xnan+xb=0，說明a1，a2，...an，b線性相關，同理x=0，可得a1，a2，....an，r線性相關。若x，y都不為零，兩邊除以x可得-b=x1/x)a1+(x2/x)a2+...+(xn/x)an+(y/x)r，這表示b可以用a1，a2，....an，r.表示。若除以y可證明r可以用a1，a2，....an，b表示。這就說明a1，a2，....an，b與a1，a2，....an，r等價。綜合可得命題得證。

當A和B為同型矩陣，且r（A）=r（B）時，A，B一定等價。

在線性代數和矩陣論中，有兩個m×n階矩陣A和B，如果這兩個矩陣滿足B=QAP（P是n×n階可逆矩陣，Q是m×m階可逆矩陣），那麼這兩個矩陣之間是等價關係。也就是說，存在可逆矩陣（P、Q)，使得A經過有限次的初等變換得到B。

● ● 矩陣A和A等價(反身性）；

● ● 矩陣A和B等價，那麼B和A也等價(等價性）；

● ● 矩陣A和B等價，矩陣B和C等價,那麼A和C等價（傳遞性）；

● ● 矩陣A和B等價，那麼IAI=KIBI。(K為非零常數)

● ● 具有行等價關係的矩陣所對應的線性方程組有相同的解對於相同大小的兩個矩形矩陣，它們的等價性也可以通過以下條件來表徵：

（1）矩陣可以通過基本行和列操作的而彼此變換。

徠（2）當且僅當它們具有相同的秩時，兩個矩陣是等價的。

其中對角線上的1的數目等於k。這是史密斯正則形式的一個特例，它將這個概念概括在向量空間上。