算籌
算籌
根據史書的記載和考古材料的發現,古代的算籌實際上是一根根同樣長短和粗細的小棍子,一般長為13--14cm,徑粗0.2~0.3cm,多用竹子製成,也有用木頭、獸骨、象牙、金屬等材料製成的,大約二百七十幾枚為一束,放在一個布袋裡,系在腰部隨身攜帶。
需要記數和計算的時候,就把它們取出來,放在桌上、炕上或地上都能擺弄。別看這些都是一根根不起眼的小棍子,在中國數學史上它們卻是立有大功的。而它們的發明,同樣經歷了一個漫長的歷史發展過程。
算籌
算籌的發明就是在以上這些記數方法的歷史發展中逐漸產生的。它最早出現在何時,已經不可查考了,但至遲到春秋戰國;算籌的使用已經非常普遍了。前面說過,算籌是一根根同樣長短和粗細的小棍子,那麼怎樣用這些小棍子來表示各種各樣的數目呢?

算籌
算籌
用算籌進行乘法計算,先擺乘數於上,再擺被乘數於下,並使上數的末位與下數的首位對齊,按從左到右的順序用上數首位乘下數各位,把乘得的積擺在上下兩數中間,然後將上數的首位去掉、下數向右移動一位,再以上數第二位乘下數各位,加入中間的乘積,並去掉上數第二位。直到上數各位用完,中間的數便是結果。下面以183×26為例具體說明一下:
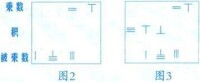
1.把乘數26擺在上面,被乘數183擺在下面,被乘數的個位與乘數的十位對齊,中間留有空餘,準備擺乘得的積(如圖2);
2.從高位乘起,用乘數十位上的2乘被乘數183,得3660,擺在中間,積的數位與被乘數對齊(如圖3,積的個位0用空位表示);
算籌

算籌
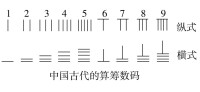
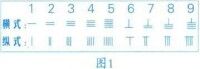
按照中國古代的籌算規則,算籌記數的表示方法為:個位用縱式,十位用橫式,百位再用縱式,千位再用橫式,萬位再用縱式等等(到搜狗可以查)這樣從右到左,縱橫相間,以此類推,就可以用算籌表示出任意大的自然數了。由於它位與位之間的縱橫變換,且每一位都有固定的擺法,所以既不會混淆,也不會錯位。毫無疑問,這樣一種算籌記數法和現代通行的十進位制記數法是完全一致的。
中國古代十進位制的算籌記數法,在世界數學史上是一個偉大的創造。把它與世界其他古老民族的記數法作一比較,其優越性是顯而易見的。古羅馬的數字系統沒有位值制,只有七個基本符號,如要記稍大一點的數目就相當繁難。古美洲瑪雅人雖然懂得位值制,但用的是20進位;古巴比倫人也知道位值制,但用的是60進位。20進位至少需要19個數碼,60進位則需要59個數碼,這就使記數和運算變得十分繁複,遠不如只用9個數碼便可表示任意自然數的十進位制來得簡捷方便。中國古代數學之所以在計算方面取得許多卓越的成就,在一定程度上應該歸功於這一符合十進位制的算籌記數法。馬克思在他的《數學手稿》一書中稱十進位記數法為"最妙的發明之一",當然是一點也不過分。
在算籌計數法中,以縱橫兩種排列方式來表示單位數目的,其中1-5均分別以縱橫方式排列相應數目的算籌來表示,6-9則以上面的算籌再加下面相應的算籌來表示。表示多位數時,個位用縱式,十位用橫式,百位用縱式,千位用橫式,以此類推,遇零則置空。這種計數法遵循十進位制。算籌的出現年代已經不可考,但據史料推測,算籌最晚出現在春秋晚期戰國初年(公元前722年~公元前221年)。
兩千多年前我們的祖先就懂得了這樣精妙的計算,真是神奇!在這當中,算籌功不可沒,它是在珠算發明以前中國獨創並且是最有效的計算工具。中國古代數學的早期發達與持續發展都是受惠於算籌的。
