縱內彈性模數
縱內彈性模數
受載機械零件或構件的材料,當應力不超過材料的比例極限時,應力與其相應的應變之比為一常數,並且與方向、位置無關。在材料力學中,彈性模量有下述3種:彈性模量E(又稱縱向彈性模量、楊氏彈性模量)為單向正應力σ與其方向上的應變ε之比;剪切彈性模量G為剪應力τ與其相應的剪應變γ之比;體彈性模量K為作用在彈性體全部表面上的均勻分佈應力p(例如水壓)與其相應的體應變之比。由單向正應力引起的彈性桿件的橫嚮應變與軸向(縱向)應變ε之比的絕對值μ稱為泊松比。E、G、K、μ 4個參數中,只要給定任意2個參數,就可以查得其餘2個參數。彈性模量用於計算應力與應變。
縱向彈性模數,又稱揚氏模數或彈性模量、彈性模數。即應力與應變之間的關係(應力與應變之比),服從胡克定律呈直線的關係。
縱內彈性模數
縱內彈性模數
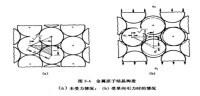
圖1 金屬原子結晶構造
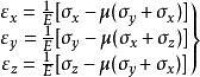
縱內彈性模數
剪切彈性模數G,簡稱剪切模數,它是剪應力τ與剪應變γ之比。
積變模數K,又稱體積彈性模數,為平均正應力(靜液壓力)與體積應變之比。
在E、G、K、μ四個參數中,已知任意兩個,就可查表得知另外兩個參數。(見下表)
| 彈性模量間的關係 | |||||
|---|---|---|---|---|---|
| E,μ | G,μ | E,G | E,K | G,K | |
| E | E | 2(1+μ)G | E | E | 9KG/(3K+G) |
| G | E/2(1+μ) | G | G | 3EK/(9K-E) | G |
| K | E/3(1-2μ) | 2(1+γ)G/3(1-2γ) | EG/3(G-E) | K | K |
| μ | μ | μ | (E-2G)/2G | (3K-E)/6K | (3K-2G)/3(2K+G) |