arccos

數學術語

arccos表示的是反三角函數中的反餘弦。一般用於表示當角度為非特殊角時。由於是多值函數，往往取它的單值，值域為[0，π]，記作y=arccosx，我們稱它叫做反三角函數中的反餘弦函數的主值。

目錄

1應用示例 2其他公式

應用示例

arccos

arccos

反三角函數中的反餘弦。意思為：餘弦的反函數，函數為y=arccosx，函數圖像如右下圖。

就是已知餘弦數值，反求角度，如cos(a)=b，則arccos(b)=a；它的值是以弧度表達的角度。定義域：[-1，1]。

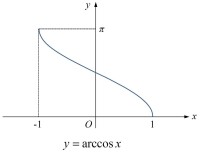
函數圖像如右下圖。

其他公式

cos(arcsinx)=√（1-x^2）

arcsin(-x)=-arcsinx

arccos(-x)=π-arccosx

arctan(-x)=-arctanx

arccot(-x)=π-arccotx

arcsinx+arccosx=π/2=arctanx+arccotx

sin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=x

當x∈[-π/2，π/2]，有arcsin(sinx)=x

x∈[0，π]，arccos(cosx)=x

x∈(-π/2，π/2)，arctan(tanx)=x

x∈(0，π)，arccot(cotx)=x

x>0，arctanx=π/2-arctan1/x，arccotx類似

若(arctanx+arctany)∈(-π/2，π/2)，則arctanx+arctany=arctan((x+y)/(1-xy))

目錄