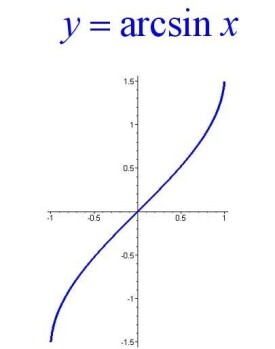
反三角函數

反三角函數（inverse trigonometric function）是一類初等函數。指三角函數的反函數。由於基本三角函數具有周期性，所以反三角函數是多值函數。這種多值的反三角函數包括：反正弦函數、反餘弦函數、反正切函數、反餘切函數、反正割函數、反餘割函數，分別記為。但是，在實函數中一般只研究單值函數，只把定義在包含銳角的單調區間上的基本三角函數的反函數，稱為反三角函數，這是亦稱反圓函數。為了得到單值對應的反三角函數，人們把全體實數分成許多區間，使每個區間內的每個有定義的 y 值都只能有惟一確定的 x 值與之對應。為了使單值的反三角函數所確定區間具有代表性，常遵循如下條件：

1、為了保證函數與自變數之間的單值對應，確定的區間必須具有單調性；

2、函數在這個區間最好是連續的（這裡之所以說最好，是因為反正割和反餘割函數是尖端的）；

3、為了使研究方便，常要求所選擇的區間包含0到的角；值的反三角函數相區別，在記法上常將中的改記為，例如單值的反正弦函數記為。

為限制反三角函數為單值函數，將反正弦函數的值y限在，將y作為反正弦函數的主值，記為；相應地，反餘弦函數的主值限在；反正切函數的主值限在；反餘切函數的主值限在。

正弦函數在上的反函數，叫做反正弦函數。記作，表示一個正弦值為x的角，該角的範圍在區間內。定義域[-1，1] ，值域。

餘弦函數在上的反函數，叫做反餘弦函數。記作，表示一個餘弦值為x的角，該角的範圍在區間內。定義域[-1，1] ，值域。

正切函數在上的反函數，叫做反正切函數。記作，表示一個正切值為的角，該角的範圍在區間內。定義域R，值域。

餘切函數在上的反函數，叫做反餘切函數。記作，表示一個餘切值為x的角，該角的範圍在區間內。定義域R，值域。

正割函數在上的反函數，叫做反正割函數。記作，表示一個正割值為的角，該角的範圍在區間內。定義域,值域。

餘割函數在上的反函數，叫做反餘割函數。記作，表示一個餘割值為的角，該角的範圍在區間內。定義域,值域。

（1）

或

（2）

（3）

（4）

（5）

（6）

（7）