值域

函數經典定義中，因變數的取值範圍叫做這個函數的值域，在函數現代定義中是指定義域中所有元素在某個對應法則下對應的所有的象所組成的集合。即

常見函數值域：

的值域為R

的值域為

的值域為

時，值域為；

當時，值域為

的值域為

的值域為R

在解決問題的過程中，數學家往往不是直接解決原問題，而是對問題進行變形、轉化，直至把它化歸為某個(些)已經解決的問題，或容易解決的問題。把所要解決的問題，經過某種變化，使之歸結為另一個問題*，再通過問題*的求解，把解得結果作用於原有問題，從而使原有問題得解，這種解決問題的方法，我們稱之為化歸法；

解數學題時，把某個式子看成一個整體，用一個變數去代替它，從而使問題得到簡化，這叫換元法。換元的實質是轉化，關鍵是構造元和設元，理論依據是等量代換，目的是變換研究對象，將問題移至新對象的知識背景中去研究，從而使非標準型問題標準化、複雜問題簡單化，變得容易處理。換元法又稱輔助元素法、變數代換法。通過引進新的變數，可以把分散的條件聯繫起來，隱含的條件顯露出來，或者把條件與結論聯繫起來。或者變為熟悉的形式，把複雜的計算和推證簡化。它可以化高次為低次、化分式為整式、化無理式為有理式、化超越式為代數式，在研究方程、不等式、函數、數列、三角等問題中有廣泛的應用。例如在分解時，可以令,則．例2，令原方程可寫為解得所以所以注意：換元后勿忘還原；

利用函數和他的反函數定義域與值域的互逆關係，通過求反函數的定義域，得到原函數的值域；

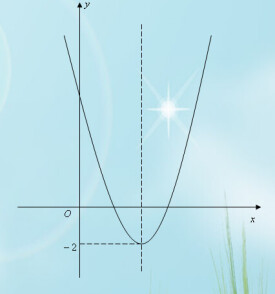
根據函數圖象，觀察最高點和最低點的縱坐標。

利用二次函數的配方法求值域，需注意自變數的取值範圍。

利用二次函數的頂點式或對稱軸，再根據單調性來求值域。

若函數存在反函數，可以通過求其反函數，確定其定義域就是原函數的值域。

包含代數換元、三角換元兩種方法，換元后要特別注意新變數的範圍。

判別式法即利用二次函數的判別式求值域。

設複合函數為f[g(x)],g(x)為內層函數,為了求出f的值域，先求出g(x)的值域,然後把g(x)看成一個整體，相當於f(x)的自變數x，所以g(x)的值域也就是f[g(x)]的定義域，然後根據f(x)函數的性質求出其值域；

利用基本的三角關係式，進行簡化求值。例如，求證：.直接計算麻煩用三角代換法比較簡單：做法：設則因為我們知道cos(y-x)小於等於1，所以不等式成立。

基本不等式法：利用求函數值域時，要時刻注意不等式成立的條件，即“一正，二定，三相等”。

把分子分母中都有的未知數變成只有分子或者只有分母的情況，由於分子分母中都有未知數與常數的和，所以一般來說我們分拆分子，這樣把分子中的未知數變成分母的倍數，然後就只剩下常數除以一個含有未知數的式子

定義域、對應法則、值域是函數構造的三個基本“元件”。平時數學中，實行“定義域優先”的原則，無可置疑。然而事物均具有二重性，在強化定義域問題的同時，往往就削弱或淡化了，對值域問題的探究，造成了一手“硬”一手“軟”，使學生對函數的掌握時好時壞，事實上，定義域與值域二者的位置是相當的，絕不能厚此薄彼，何況它們二者隨時處於互相轉化之中（典型的例子是互為反函數的定義域與值域的相互轉化）。如果函數的值域是無限集的話，那麼求函數值域不總是容易的，反靠不等式的運算性質有時並不能奏效，還必須聯繫函數的奇偶性、單調性、有界性、周期性來考慮函數的取值情況。才能獲得正確答案，從這個角度來講，求值域的問題有時比求定義域問題難。實踐證明，如果加強了對值域求法的研究和討論，有利於對定義域內函數的理解，從而深化對函數本質的認識。

“範圍”與“值域”是我們在學習中經常遇到的兩個概念。許多同學常常將它們混為一談，實際上這是兩個不同的概念。“值域”是所有函數值的集合（即集合中每一個元素都是這個函數的取值），而“範圍”則只是滿足某個條件的一些值所在的集合（即集合中的元素不一定都滿足這個條件）。也就是說:“值域”是一個“範圍”，而“範圍”卻不一定是“值域”。

設A是線性空間V的一個線性變換，由A的全體象組成的集合稱為A的值域，記為AV，且有

所以AV對於線性運算封閉，當然，AV非空，因此AV是V的子空間。

又有AV包含於V可以看出AV是A的不變子空間。