開普勒第一定律
橢圓定律
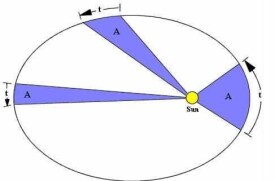
開普勒第一定律,也稱橢圓定律、軌道定律:每一行星沿各自的橢圓軌道環繞太陽,而太陽則處在橢圓的一個焦點上。
開普勒第一定律是由德國天文學家約翰尼斯·開普勒提出的,他於1609年在他出版的《新天文學》科學雜誌上發表了關於行星運動的兩條定律,又於1618年,發現了第三條定律。在此定律出現以前,人們認為天體的運行軌道是:“完美的圓形”。在天文學與物理學上,開普勒的定律給予亞里士多德派與托勒密派極大的挑戰。開普勒主張地球是不斷地移動的;行星軌道不是圓形的,而是橢圓形的;行星公轉的速度不等恆。這些論點,大大地動搖了當時的天文學與物理學。
經過幾乎一個世紀的研究,物理學家終於能夠運用物理學理論解釋原理。牛頓應用他的第二定律和萬有引力定律,在數學上嚴格地證明了開普勒定律,也讓人了解了其中的物理意義。因此,開普勒的三條行星運動定律改變了整個天文學,徹底摧毀了托勒密複雜的宇宙體系,完善並簡化了哥白尼的日心說,他因此成為十七世紀科學革命的關鍵人物。
開普勒在《宇宙和諧論》發表的表述:每一個行星都沿各自的橢圓軌道環繞太陽,而太陽則處在橢圓的一個焦點中。
設定
這樣,角速度是
對時間微分和對角度微分有如下關係:
根據上述關係,徑向距離 對時間的導數為:
再求一次導數:
代入徑向運動方程, ,有
將此方程除以 ,則可得到一個簡單的常係數非齊次線性全微分方程來描述行星軌道:
為了解這個微分方程,先列出一個特解
再求解剩餘的常係數齊次線性全微分方程,
它的解為
這裡,與 是常數。合併特解和與齊次方程解,可以得到通解
選擇坐標軸,讓 。代回 ,
其中, 是離心率。
這是圓錐曲線的極坐標方程,坐標系的原點是圓錐曲線的焦點之一。假若 ,則 所描述的是橢圓軌道。這證明了開普勒第一定律。
開普勒1596年出版《宇宙的神秘》一書受到第谷的賞識,應邀到布拉格附近的天文台做研究工作。1600年,到布拉格成為第谷的助手。次年第谷去世,開普勒成為第谷事業的繼承人。
第谷去世后開普勒用很長時間對第谷遺留下來的觀測資料進行分析,他在分析火星的公轉時發現,無論按哥白尼的方法還是按托勒密或第谷的方法,算出的軌道都不能同第谷的觀測資料相吻合,他堅信觀測的結果,於是他想到火星可能不是作當時人們認為的勻速圓周運動,他改用各種不同的幾何曲線來表示火星的運動軌跡,終於發現了“火星沿橢圓軌道繞太陽運行。
開普勒在1619年出版的《宇宙和諧論》發表該定律。
開普勒第三定律:是指繞以太陽為焦點的橢圓軌道運行的所有行星,其橢圓軌道半長軸的立方與周期的平方之比是一個常量。這裡,a是行星公轉軌道半長軸,T是行星公轉周期,K是常數,其大小隻與中心天體的質量有關。
約翰內斯·開普勒(1571年12月27日-1630年11月15日),德國天文學家、數學家。開普勒是十七世紀科學革命的關鍵人物。他最為人知的開普勒定律,是後代的天文學家根據他的著作《新天文學》、《世界的和諧》、《哥白尼天文學概要》萃取而成的。這些傑作對艾薩克·牛頓影響極大,啟發牛頓後來想出牛頓萬有引力定律。
開普勒曾在奧地利格拉茨的一家神學院擔任數學教師。後來,他成了天文學家第谷·布拉赫的助手,並最終成為皇帝魯道夫二世及其兩任繼任者馬蒂亞斯和費迪南二世的皇家數學家。他還曾經在奧地利林茨擔任過數學教師及華倫斯坦將軍的顧問。
開普勒的第一部主要天文學作品——《宇宙的神秘》是第一部捍衛哥白尼學說並且公開發表的作品。他提出的“多面體—球體”假說雖然被證明是錯誤的,但這他是清除哥白尼學說中殘留的托勒密理論的第一步。
1600年2月4日,開普勒在伊澤拉河畔貝納特基見到了第谷·布拉赫。伊澤拉河畔貝納特基是第谷的新天文台所在地。開普勒以客人的身份在這裡住了兩個月,同時分析了第谷的一些火星發現。差不多1601年一整年,他得到了第谷的直接資助。1601年10月24日,第谷出人意料的逝世了。兩天之後,開普勒被委任成為他的繼任者,作為皇家數學家負責完成第谷未完成的工作。
《新天文學》是開普勒根據第谷的方向進行的火星軌道研究發展的頂峰。開普勒運用等分點對火星軌道進行重複近似,但是他對自己有點不準確的結果仍感到不滿意:在某些點,這個模型與數據的差異達到8弧分。在經歷大約40次的嘗試失敗以後,1605年初,他想到了橢圓形這個概念。在發現橢圓形軌道非常適用於火星的數據之後,他推斷出關於行星運動的第一定律。然而,他未將該數學分析擴展到火星之外。當年年底,他完成了《新天文學》的手稿。開普勒在1619年出版的《宇宙和諧論》重新發表了開普勒三條定律。
在他生命的最後幾年,開普勒花了很多時間旅行。他於1630年11月15日在雷根斯堡去世,並安葬在那裡;它安葬的地點在瑞典軍隊毀壞墓地之後不復存在。只有開普勒自創的墓誌銘還流傳下來:
Mensus eram coelos, nunc terrae metior umbras
Mens coelestis erat, corporis umbra iacet.
“仰天之高,俯地之深。“
”九霄安魂,一隅安身。”