牛頓內摩擦定律
牛頓內摩擦定律
1686年英國科學家牛頓給出了表徵內摩擦力的定律,他指出:1、內摩擦力正比於流層移動的相對速度;2、內摩擦力正比於流層間的接觸面積;3、內摩擦力隨流體的物理性質而改變;4、內摩擦力與正壓力無關。
一切真實流體中,由於分子的擴散或分子間相互吸引的影響,使不同流速的流體之間有動量交換髮生,因此,在流體內部兩流層的接觸面上產生內摩擦力。這種力與作用面平行,故又稱流動切應力,或粘性力。粘性力的方向,對流速大的流體層而言,它與流速方問相反,是阻礙流動的力;相應地,對流速小的流體層而言則是促使其加速的力。粘性力的大小可由牛頓內摩擦定律確定。
考慮一種流體,它介於面積相等的兩塊大的平板之間,如《平行平板示意圖》所示,這兩塊平板處處以一很小的距離分隔開,該系統原先處於靜止狀態。假設讓上面一塊平板以恆定速度v在x方向上運動。
平行平板示意圖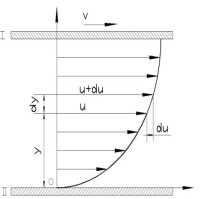

牛頓內摩擦定律
緊貼於運動平板下方的一薄層流體也以同一速度運動。當不太大時,板間流體將形成穩定層流。靠近運動平板的液體比遠離平板的液體具有較大的速度,且離平板越遠的薄層,速度越小,至固定平板處,速度降為零。
速度按某種曲線規律連續變化。這種速度沿距離的變化稱為速度分佈。
設某一流層速度為,與其相鄰流層速度為,為其流速變化值,設流層間沿軸距離差為,若兩板間的距離很小,則兩板間的流速變化無限接近線性,即可化為流速梯度。
設F為流體各層間的內摩擦力,流體間接觸面積為。
大量實驗證明,流體的內摩擦力大小與流體性質有關,與流體速度變化梯度和接觸面積成正比。
若將比例係數設為。
則各物理量關係滿足:
此理論為牛頓內摩擦定律。
上式說明流體在流動過程中流體層間所產生的剪應力與法向速度梯度成正比,與壓力無關。流體的這一規律與固體表面的摩擦力規律不同。
● ● 僅適用於層流流動,不適用於湍流流動;
● ● 僅適用於牛頓流體,不適用於非牛頓流體。
工程學中,常令г為單位面積上的內摩擦力,即摩擦應力(又稱切應力),於是得到下式
式中:τ為單位面積上的摩擦應力,也叫做剪應力,Pa或N/㎡;
F為相鄰流體層間內摩擦力,N;
A為流體層接觸面積,㎡;
μ為與流體性質相關的比例係數,通常稱為動力黏性係數,或稱動力粘度,Pa*s或kg/(m*s)。
du/dy為速度梯度,1/s;
牛頓內摩擦定律又稱黏性定律。
1845年,英國數學家斯托克斯提出了3個假設,將牛頓內摩擦定律推廣到黏性流體的任意流動狀態中。
1、流體是連續的,它的應力張量是應變率張量的線性函數,與流體的平動和轉動無關。
2、流體是各向同性的,流體中的應力與應變率的線性關係與坐標系的選擇和位置無關
3、當流體靜止時,應變率為零,流體中的應力只有正應力,切應力為零。
實驗證明上述假設對大多數常見流體是正確的。根據斯托克斯假設,可將應力張量與應變率張量的線性關係表示為:
在直角坐標系下,廣義牛頓內摩擦定律的分量形式可寫為:
如果流體的應力與應變率之間不能用廣義牛頓內摩擦定律來描述,則這種流體就稱為非牛頓流體。例如,油漆、泥漿、血液等均屬於非牛頓流體。
