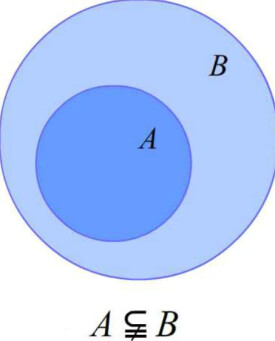
真子集

子集

一般地，對於兩個集合A、B，如果集合A中任意一個元素都是集合B中的元素，我們就說這兩個集合有包含關係，稱集合A為集合B的子集（subset）。記作A⊆B（或B⊇A），讀作“A包含於B”（或“B包含A”）。

即，對於集合A與B，∀x∈A有x∈B，則A⊆B。可知任一集合A是自身的子集，空集是任一集合的子集。

真子集

如果集合A⊆B，存在元素x∈B，且元素x不屬於集合A，我們稱集合A與集合B有真包含關係，集合A是集合B的真子集（proper subset）。記作A⊊B（或B⊋A），讀作“A真包含於B”（或“B真包含A”）。

即：對於集合A與B，∀x∈A有x∈B，且∃x∈B且x∉A，則A⊊B。空集是任何非空集合的真子集。

非空真子集：如果集合A⊊B，且集合A≠∅，集合A是集合B的非空真子集（nonvoid proper subset）。

真子集與子集的區別：

● 子集就是一個集合中的全部元素是另一個集合中的元素，有可能與另一個集合相等；

● 真子集就是一個集合中的元素全部是另一個集合中的元素，但不存在相等。

● 所有亞洲國家組成的集合是地球上所有國家組成的集合的真子集；所有自然數的集合是所有整數的集合的真子集（即N⊊Z）；{1, 3} ⊊ {1, 2, 3, 4}，{1, 2, 3} ⊊ {1, 2, 3, 4}； ∅⊊{∅}。但不能說{1, 2, 3}⊊ {1, 2, 3}。

● 設全集I為{1, 2, 3}，則它的子集可以是{1}、{2}、{3}、{1, 2}、{1, 3}、{2, 3}、{1, 2, 3}、∅；而它的真子集只能為{1}、{2}、{3}、{1, 2}、{1, 3}、{2, 3}、∅。它的非空真子集只能為{1}、{2}、{3}、{1, 2}、{1, 3}、{2, 3}。

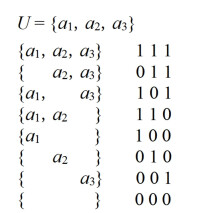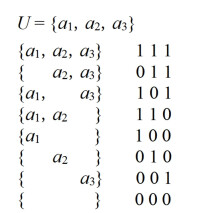
命題1：若集合A有n個元素，則集合A的子集個數為2，且有2-1個真子集，2-2個非空真子集。

證明：設元素編號為1, 2, ... n，每個子集對應一個長度為n的二進位數（規定數的第 i 位為1表示元素i在集合中，0表示元素i 不在集合中。如全集U={e1, e2, e3, e4, e5}，則{e1,e2,e3,e4,e5} ↔ 11111，{e2,e3,e4} ↔ 01110，{e4} ↔ 00010）。即其子集為00...0（n個0） ~ 11...1（n個1）。易知一共有2個數，因此對應2個子集。去掉11...1（即表示原來的集合A）則有2-1個真子集，再去掉00...0（表示空集）則有2-2個非空真子集。

命題2：空集是任意集合的子集。

證明：給定任意集合A，要證明∅是A 的子集。這要求給出所有∅的元素是A 的元素；但是，∅沒有元素。

對有經驗的數學家們來說，推論“∅沒有元素，所以∅的所有元素是A 的元素”是顯然的；但對初學者來說，有些麻煩。換一種思維將有所幫助，為了證明∅不是A 的子集，必須找到一個元素，屬於∅，但不屬於A。因為∅沒有元素，所以這是不可能的。因此∅一定是A 的子集。

這個命題說明：包含是一種偏序關係。

命題3：若 A，B，C是集合，則：

自反性: A⊆A，反對稱性: A⊆ B且 B⊆ A，當且僅當A= B，傳遞性: 若 A⊆ B且 B⊆ C則 A⊆ C。這個命題說明：對任意集合 S，S的冪集按包含排序是一個有界格，與上述命題相結合，則它是一個布爾代數。

命題4：若 A，B，C是集合 S的子集，則：

存在一個最小元和一個最大元： ∅ ⊆ A⊆ S（ ∅⊆A由命題2給出）。存在並運算: A⊆ A∪B若 A⊆ C且 B⊆ C則 A∪B⊆ C存在交運算: A∩B⊆ A若 C⊆ A且 C⊆ B則 C⊆ A∩B。這個命題說明：表述 "A⊆ B" 和其他使用並集，交集和補集的表述是等價的，即包含關係在公理體系中是多餘的。

命題5: 對任意兩個集合 A和 B，下列表述等價：A⊆ B A∩ B= A A∪ B= B A− B=∅ B′ ⊆ A′。