排序問題
排序問題
排序問題(sequencing problem)亦稱工件加工日程表問題,是一類典型的組合優化問題。設用m台機器加工n個工件,給定了加工每個工件所用機器的次序,以及每台機器加工每個工件所需要的時間、問題是確定工件在每台機器上的加工次序以使預先選定的目標函數達到最小,這個目標函數通常是完成時間、平均完成時間、機器的空間時間等的一個非降函數。排序問題有兩個類型:1.流水作業,這時要求每個工作在機器上的加工次序都一樣;2.工件作業,這時每個工件在機器上的加工次序不必一致。流水作業可以看做是工件作業的一種特殊情形,三台或以上機器的排序問題多為NP完全問題。因此是很困難的。
排序問題已被廣泛應用於生產管理、計算機系統、運輸調度等領域。排序問題是一類重要的組合優化問題。一般來說,凡是有多個不同的任務要完成,就有作業排序與作業計劃問題。幾批不同的工件要加工,幾個程序等待要運行,幾個問題要處理等,都有作業排序。這些問題的共同特徵是要將不同的工作任務安排一個執行的順序和時間.使得目標最優化。所以.作業排序實質上是要解決如何按時間的先後,將有限的資源分配給不同的工作任務,使預定的目標最優化的問題。
需要說明的是,在生產運作管理中常用到編製作業計劃、排序、調度、派工、控制、趕工等名詞。一般來說,作業排序只確定工件在機器上的加工順序,而編製作業計劃不僅確定工件的加工順序,而且還包括確定每個工件的開始時間和完成時間,這樣才能指導工人的生產活動。由於當各台機器上工件的加工順序確定后,就可以按最早可能開始時間安排所有工件的計劃,這樣初始可行的作業計劃就可以編製好,因而編製作業計劃的問題之一就是作業排序問題。派工是按作業計劃的要求,將具體的牛產任務安排到具體的機器上並交給相應的操作工人負責;控制是監控實際生產過程.並使其和計劃保證一致的過程;調度是在加工製造發生之後,發現實際進度已經偏離計劃而採取的調配資源的行動,調度屬於控制的範圍;而 趕工是在實際進度已經落後於計劃進度時採取的追趕進度的行動,趕工屬於調度的範圍。如火車時刻表是事先確定的一種作業計劃,各列火車都按該計劃來執行;在實際執行過程需要監控所有火車運行情況,根據這些運行信息相應採取措施以確保計劃的完成,這種監控採取的預防和實際措施的過程就是 控制;其中實際運行情況偏離了計劃所採取的措施就是調度;如果火車發生晚點,採取加快運行速度來趕上計劃時間就是趕工。
最初的排序研究與應用主要是針對加工製造企業,一般使用機器、工件、加工路線、工序和加工時間來描述一個排序作業的任務。即假定有n個工件要按一定的加工路線經過m台機器加工,其中加工路線是由工件加工的工藝過程決定的,是工件加工在技術上的約束,是工件所需要的加工工序的順序。而排序就是確定這n個工件在m台機器上加工的先後順序。隨著排序在其他各行各業的應用,原有的“機器”、“工件”、“工序”和“加工時間”的意義已經發生了變化,如“機器”的意義已經擴展到“服務者”,“工件”則泛指“服務對象”,“工序”則指“服務活動”,“加工時間”則是“服務時間”。如計算機網路的伺服器(機器)同時接到多個電郵請求(工件),處理后發到請求的用戶信箱;多艘輪船(工件)同時要停靠碼頭(機器);維修工人(機器)維修多個機器設備(工件)等。
只有一台機器的排序問題稱為 單機排序問題,否則稱為多機排序問題。
在多機問題中機器分為兩大類:通用平行(parallel)機和 專用串聯(dedicated)機,如果所有機器的功能相同,稱為 同類機或 平行機,即一個工件需要在多台平行機的一個機器上加工一次;而串聯機則是機器具有不同的功能,工件需要在不同的機器上加工。
平行機又可分成3類:具有相同速度的同速(identical)機、具有不同加工速度但此速度不依賴於工件的恆速( uniform)機和隨加工的工件不同加速度也不同的變速(unrelated)機。
串聯機也可分為3類:第一個工件以特定的相同機器順序加工的流水作業(flow shop)、工件依次在機器上加工的次序可以任意的開放作業(open shop)和每一工件以各自特定的機器次序進行加工的單件作業(job shop)。
還有一類更複雜的情況,就是柔性流水作業(flexible flow shop),它是流水作業和平行機的推廣。在柔性流水作業中,有多類機器,每個工件有多道工序,每道工序需要在每類機器中的一台機器上加工,且每個工件的加工順序相同。機器的分類情況見圖1 。
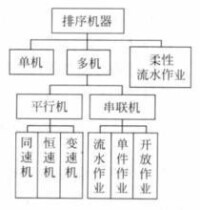
圖1 機器類型
對不允許中斷加工的情況來說,一個工件( )在一台機器( )上連續加工的過程稱為 工序(operation)。按工件到達車間的不同,可以將排序分為靜態和動態兩種。當進行排序時所有工件都已經到達,可以一次對它們進行排序,這是 靜態排序問題;若工件是陸續到達的,要隨時對它們進行排序,這是 動態排序問題。
排序中的約束條件,主要指的是工件的性質以及它們在加工過程中的要求和限制。
1) 加工時間
一個工件的加工時間: ;n個工件的加工時間則用矩陣來表示:
式中: ——工件 在機器i 上所需要的加工時間。
2) 到達時間(arrival time)或就緒時間(ready time)
到達時間或就緒時間 是工件已經準備好可以馬上被加工的時間。若所有工件的就緒時間相同,則取。
3) 工件工期(due date)或截止期限(deadline)
工期表示對工件限定的完工時間。若不按期完工,就會受到一定的懲罰。絕對不允許延誤的工期稱為截止期限。
4) 工件權重(weight)
工件權重是相對於其他工件而言工件的重要性程度。
用表示工件的完工時間。一般來說,要使完工時間的函數達到極小化。在排序問題中,目標函數主要有以下幾種。
1) 最大完工時間或時間表長(schedule length,make-span)
時間表長可定義為:,即為最後一個被加工完的工件的完工時間。
2) 加權流程時間(weighted flow time)和加權完工時間
一個工件的流程時間是指工件從到達系統開始一直到加工完為止的時間,包括在系統中的等待時間和加工時間:。
系統的平均加權流程時間:。
將上述平均流程時間轉換一下:由於第二項是常數,第一項的分母也是常數,因此極小化平均加權流程時間相當於極小化總加權完工時間(total weighted completion time):
3) 最大延誤時間(maximum lateness)
工件的延誤時間定義為最大延誤時間。
4) 加權總誤工(total weighted tardiness)
一個工件當其完工時間大於其完工期限時稱為誤工:
加權總誤工:
5) 加權誤工工件數(weighted number of tardy jobs)
用0/1來表示某工件是否誤工:
加權誤工件數:
總之,在排序中,工件是被加工的對象,是要完成的任務;機器是提供加工的對象,是完成任務所需要的資源;排序是安排一個時間表,以在一定約束條件下對工件和機器按時間進行分配和安排次序,使某一或一些目標達到最優。
排序問題的類別有多種劃分方法,如前面按機器、按工件有不同的劃分方法,另外根據參數的性質還可以劃分為確定型與隨機型排序,即加工時間和其他有關參數是已經知道的、確定的量,就稱為 確定型排序;而加工時間和相關參數是隨機型的量則稱為 隨機型排序。由機器、工件、加工參數和目標函數的不同特徵及其他方面的差別,構成了多種不同的排序問題。這裡採用國際上使用的 三參數表示方法來描述排序問題,即。
域表示機器的數量、類型和環境:,其中,各符號分別代表單機、同速機、恆速機、自由作業、流水作業、單件作業和柔性流水作業;,分別表示機器的數目不確定和有m台機器。
域表示工件的性質、加工要求和限制,資源的種類、數量和對加工的影響等,它可以同時包含多項,可能的主項有:(工件有不同的到達時間)、(工件順序加工的設備調整時間)、prmp(允許中斷)等。
域表示要優化的目標函數:(時間表長)、(加權總完工時間)、(最大延誤時間)、(加權總誤工)、(加權誤工件數)等。
如表示單機排序問題,目標函數是總延誤時間最小;表示有m台同速機的排序問題,目標函數是極小化時間表長;而表示一個由m台機器組成的流水作業排序問題,每個作業的所有工序的加工時間都相等,目標是加權總完工時間最小;表示兩台機器單件作業排序問題,每個工件在每台機器上至多加工一次,其目標函數是時間表長最小。
排序問題是一類組合優化問題,由於在實際生產中,排序問題中的機器、工序、資源都是有限的,絕大部分排序問題是從有限個可行解中找出一個最優解,使目標函數達到極小。
車間作業計劃可能存在著很多可行的作業計劃安排方法,其中各工序都按最早可能加工或完工時間安排的作業計劃稱為 半能動計劃( semi-active schedule);若半能動計劃中任何一台機器的每段空閑時間都不足以加工一道加工工序的,稱為 能動作業計劃(active schedule);若在能動計劃中,沒有任何延遲(delay)現象出現,則稱為 無延遲作業計劃(non-delay schedule),這裡的無延遲是指如果有準備好的被加工的T序,不準許有空閑的機器出現,該計劃相當於不允許強迫機器空閑。
對於大多數排序問題,包括所有可中斷排序問題,最優排序是無延遲排序,但也有一些不可中斷的排序問題是延遲排序。