回溯法

基本思想

在包含問題的所有解的解空間樹中，按照深度優先搜索的策略，從根結點出發深度探索解空間樹。當探索到某一結點時，要先判斷該結點是否包含問題的解，如果包含，就從該結點出發繼續探索下去，如果該結點不包含問題的解，則逐層向其祖先結點回溯。（其實回溯法就是對隱式圖的深度優先搜索演演算法）。若用回溯法求問題的所有解時，要回溯到根，且根結點的所有可行的子樹都要已被搜索遍才結束。而若使用回溯法求任一個解時，只要搜索到問題的一個解就可以結束。一般表達

可用回溯法求解的問題P，通常要能表達為：對於已知的由n元組（x1，x2，…，xn）組成的一個狀態空間E={（x1，x2，…，xn）∣xi∈Si ，i=1，2，…，n}，給定關於n元組中的一個分量的一個約束集D，要求E中滿足D的全部約束條件的所有n元組。其中Si是分量xi的定義域，且 |Si| 有限，i=1，2，…，n。我們稱E中滿足D的全部約束條件的任一n元組為問題P的一個解。解問題P的最樸素的方法就是枚舉法，即對E中的所有n元組逐一地檢測其是否滿足D的全部約束，若滿足，則為問題P的一個解。但顯然，其計算量是相當大的。規律

對於許多問題，所給定的約束集D具有完備性，即i元組（x1，x2，…，xi）滿足D中僅涉及到x1，x2，…，xi的所有約束意味著j（j<=i）元組（x1，x2，…，xj）一定也滿足d中僅涉及到x1，x2，…，xj的所有約束，i=1，2，…，n。換句話說，只要存在0≤j≤n-1，使得（x1，x2，…，xj）違反d中僅涉及到x1，x2，…，xj的約束之一，則以（x1，x2，…，xj）為前綴的任何n元組（x1，x2，…，xj，xj+1，…，xn）一定也違反d中僅涉及到x1，x2，…，xi的一個約束，n≥i≥j。因此，對於約束集d具有完備性的問題p，一旦檢測斷定某個j元組（x1，x2，…，xj）違反d中僅涉及x1，x2，…，xj的一個約束，就可以肯定，以（x1，x2，…，xj）為前綴的任何n元組（x1，x2，…，xj，xj+1，…，xn）都不會是問題p的解，因而就不必去搜索它們、檢測它們。回溯法正是針對這類問題，利用這類問題的上述性質而提出來的比枚舉法效率更高的演演算法。空間樹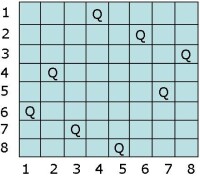回溯法首先將問題P的n元組的狀態空間E表示成一棵高為n的帶權有序樹T，把在E中求問題P的所有解轉化為在T中搜索問題P的所有解。樹T類似於檢索樹，它可以這樣構造：設Si中的元素可排成xi(1) ，xi(2) ，…，xi(mi-1) ，|Si| =mi，i=1，2，…，n。從根開始，讓T的第I層的每一個結點都有mi個兒子。這mi個兒子到它們的雙親的邊，按從左到右的次序，分別帶權xi+1(1) ，xi+1(2) ，…，xi+1(mi) ，i=0，1，2，…，n-1。照這種構造方式，E中的一個n元組（x1，x2，…，xn）對應於T中的一個葉子結點，T的根到這個葉子結點的路徑上依次的n條邊的權分別為x1，x2，…，xn，反之亦然。另外，對於任意的0≤i≤n-1，E中n元組（x1，x2，…，xn）的一個前綴I元組（x1，x2，…，xi）對應於T中的一個非葉子結點，T的根到這個非葉子結點的路徑上依次的I條邊的權分別為x1，x2，…，xi，反之亦然。特別，E中的任意一個n元組的空前綴（），對應於T的根。因而，在E中尋找問題P的一個解等價於在T中搜索一個葉子結點，要求從T的根到該葉子結點的路徑上依次的n條邊相應帶的n個權x1，x2，…，xn滿足約束集D的全部約束。在T中搜索所要求的葉子結點，很自然的一種方式是從根出發，按深度優先的策略逐步深入，即依次搜索滿足約束條件的前綴1元組（x1i）、前綴2元組（x1，x2）、…，前綴I元組（x1，x2，…，xi），…，直到i=n為止。在回溯法中，上述引入的樹被稱為問題P的狀態空間樹；樹T上任意一個結點被稱為問題P的狀態結點；樹T上的任意一個葉子結點被稱為問題P的一個解狀態結點；樹T上滿足約束集D的全部約束的任意一個葉子結點被稱為問題P的一個回答狀態結點，它對應於問題P的一個解解題步驟（1）針對所給問題，定義問題的解空間；（2）確定易於搜索的解空間結構；（3）以深度優先方式搜索解空間，並在搜索過程中用剪枝函數避免無效搜索。經典問題八皇后問題八皇后問題是能用回溯法解決的一個經典問題。八皇后問題是一個古老而著名的問題。該問題是十九世紀著名的數學家高斯1850年提出：在8X8格的國際象棋上擺放八個皇后，使其不能互相攻擊，即任意兩個皇后都不能處於同一行、同一列或同一對角線上，問有多少種擺法。引入一個整型一維數組col[]來存放最終結果，col[i]就表示在棋盤第i列、col[i]行有一個皇后，為了使程序再找完了全部解后回到最初位置，設定col[0]的初值為0，即當回溯到第0列時，說明以求得全部解，結束程序運行。為了方便演演算法的實現，引入三個整型數組來表示當前列在三個方向上的狀態：a[] a[i]=0表示第i行上還沒有皇后；b[] b[i]=0表示第i列反斜線/上沒有皇后；c[] c[i]=0表示第i列正斜線\上沒有皇后。棋盤中同一反斜線/上的方格的行號與列號相同；同一正斜線\上的方格的行號與列號之差均相同，這就是判斷斜線的依據。初始時，所有行和斜線上都沒有皇后，從第1列的第1行配置第一個皇后開始，在第m列，col[m]行放置了一個合理的皇后，準備考察第m+1列時，在數組a[]，b[]和c[]中為第m列，col[m]行的位置設定有皇后的標誌；當從第m列回溯到m-1列時，並準備調整第m-1列的皇后配置時，清除在數組a[],b[]和c[]對應位置的值都為1來確定。用回溯法解決八皇后問題的C語言程序#include#include#define Queens 8int a[Queens+1]; //八皇后問題的皇后所在每一行位置，從1開始算int main(){int i,k,flag,not_finish=1,count=0;i=1;//初始a[1]=1;printf("the possible configuration of 8 queesns are:\n");while(not_finish) //not_finsh=1:處理未結束{while(not_finish && iif(!flag) //若存在矛盾 重設第i個元素{if(a[i]==a[i-1]) //若a[i]的值已經已經一圈追上a[i-1]的值{i--; //退回一步 重新試探處理前一個元素if(i>1 && a[i]==Queens)a[i]=1; // 當a[i]為 Queens時 將a[i]的值重置elseif(i==1 && a[i]==Queens)//當第一未位的值達到Queens時結束not_finish=0;elsea[i]++;}elseif(a[i]==Queens)a[i]=1;elsea[i]++;}elseif(++i<=Queens) //若前一個元素的值為Queensif(a[i-1]==Queens)a[i]=1;else //否則元素為前一個元素的下一個值a[i]=a[i-1]+1;}if (not_finish){++count;printf((count-1)%3?"[%2d]:":"\n[%2d]:",count);for(k=1;k<=Queens;k++) //輸出結果printf("%d",a[k]);if(a[Queens-1]n thenbegint:=t+1;exit;end;for i:=1 to n dobeginx[k]:=i;if pa(k) then try(k+1);end;end;beginread(n);t:=0;try(1);write(t);end.迷宮問題回溯法解決迷宮問題C語言#include#include#define m 5#define n 6int sf=0;int mase[m][n]={{0,0,0,1,0,0},{0,1,0,0,0,0},{0,1,1,1,1,0},{0,0,0,0,0,1},{1,0,1,1,0,0}};void search(int x,int y){if((x==m-1)&&(y==n-1))sf=1;else{mase[x][y]=1;if((sf!=1)&&(y!=n-1)&&mase[x][y+1]==0)search(x,y+1);if((sf!=1)&&(x!=m-1)&&mase[x+1][y]==0)search(x+1,y);if((sf!=1)&&(y!=0)&&mase[x][y-1]==0)search(x,y-1);if((sf!=1)&&(x!=0)&&mase[x-1][y]==0)search(x-1,y);}mase[x][y]=0;if(sf==1)mase[x][y]=5;//通過路徑用數字的表示}int main(){int i=0,j=0;//clrscr();search(0,0);for(i=0;i{for(j=0;jprintf("%d",mase[i][j]);printf("\n");}system("pause");return 0;}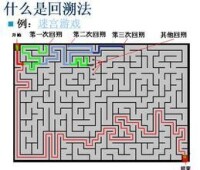

回溯法

回溯法解決迷宮問題PASCAL語言program migong;varn,k,j,x,y:integer;a:array[0..10000,0..10000] of integer;b:array[0..1000000,0..2] of integer;procedure search(x,y,i:integer);begina[x,y]:=1;if (x=n) and (y=n) thenbeginfor j:=1 to i-1 dowriteln(j,':(',b[j,1],',',b[j,2],')');writeln(i,':(',x,',',y,')');halt;end;if a[x-1,y]=0 then begin b[i,1]:=x;b[i,2]:=y;search(x-1,y,i+1);end;if a[x+1,y]=0 then begin b[i,1]:=x;b[i,2]:=y;search(x+1,y,i+1);end;if a[x,y-1]=0 then begin b[i,1]:=x;b[i,2]:=y;search(x,y-1,i+1);end;if a[x,y+1]=0 then begin b[i,1]:=x;b[i,2]:=y;search(x,y+1,i+1);end;a[x,y]:=0;end;beginread(n);for k:=1 to n dofor j:=1 to n doread(a[k,j]);for k:=0 to n+1 dobegina[k,0]:=-1;a[k,n+1]:=-1;a[n+1,k]:=-1;a[0,k]:=-1;end;x:=1;y:=1;if a[x+1,y]=0 then begin a[x,y]:=1;b[1,1]:=x;b[1,2]:=y;search(x+1,y,1);a[x,y]:=0;end;if a[x,y+1]=0 then begin a[x,y]:=1;b[1,1]:=x;b[1,2]:=y;search(x,y+1,1);a[x,y]:=0;end;end.