共找到10條詞條名為LCS的結果展開

LCS

計算機科學演演算法：最長公共子序列

LCS是Longest Common Subsequence的縮寫，即最長公共子序列。一個序列，如果是兩個或多個已知序列的子序列，且是所有子序列中最長的，則為最長公共子序列。

比如，對於char x[]="aabcd";有順序且相互相鄰的aabc是其子序列，有順序但是不相鄰的abc也是其公共子序列。即，只要得出序列中各個元素屬於所給出的數列，就是子序列。

再加上char y[]="12abcabcd";對比出才可以得出最長公共子序列abcd。

最長公共子序列問題是一個經典的計算機科學問題，也是數據比較程序，比如Diff工具，和生物信息學應用的基礎。它也被廣泛地應用在版本控制，比如Git用來調和文件之間的改變。

目錄

1定義 2定義延伸 3複雜度

4應用 5解決方法 6演算法

定義

最長公共子序列，英文縮寫為LCS（Longest Common Subsequence）。其定義是，一個序列S，如果分別是兩個或多個已知序列的子序列，且是所有符合此條件序列中最長的，則S稱為已知序列的最長公共子序列。

定義延伸

最長公共子序列（LCS）是一個在一個序列集合中（通常為兩個序列）用來查找所有序列中最長子序列的問題。這與查找最長公共子串的問題不同的地方是：子序列不需要在原序列中佔用連續的位置。而最長公共子串（要求連續）和最長公共子序列是不同的。

另外在計算機科學中，最長遞增子序列是指，在一個給定的數值序列中，找到一個子序列，使得這個子序列元素的數值依次遞增，並且這個子序列的長度儘可能地大。最長遞增子序列中的元素在原序列中不一定是連續的。許多與數學、演演算法、隨機矩陣理論（英語：random matrix theory）、表示論相關的研究都會涉及最長遞增子序列。解決最長遞增子序列問題的演演算法最低要求O(n log n)的時間複雜度，這裡n表示輸入序列的規模。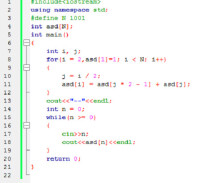

LCS

LCS

複雜度

對於一般性的LCS問題（即任意數量的序列）是屬於NP-hard。但當序列的數量確定時，問題可以使用動態規劃（Dynamic Programming）在多項式時間內解決。

最長公共子序列問題存在最優子結構：這個問題可以分解成更小，更簡單的“子問題”，這個子問題可以分成更多的子問題，因此整個問題就變得簡單了。最長公共子序列問題的子問題的解是可以重複使用的，也就是說，更高級別的子問題通常會重用低級子問題的解。擁有這個兩個屬性的問題可以使用動態規劃演演算法來解決，這樣子問題的解就可以被儲存起來，而不用重複計算。這個過程需要在一個表中儲存同一級別的子問題的解，因此這個解可以被更高級的子問題使用

應用

最長公共子序列是一個十分實用的問題，它可以描述兩段文字之間的“相似度”，即它們的雷同程度，從而能夠用來辨別抄襲。對一段文字進行修改之後，計算改動前後文字的最長公共子序列，將除此子序列外的部分提取出來，這種方法判斷修改的部分，往往十分準確。簡而言之，百度知道、百度百科都用得上。

解決方法

對於一般的LCS問題，都屬於NP問題。當數列的量為一定的時，都可以採用動態規劃去解決。

演演算法

演演算法名稱：線性DP

動態規劃的一個計算最長公共子序列的方法如下，以兩個序列X、Y為例子：

設有二維數組f[i][j]表示X的i位和Y的j位之前的最長公共子序列的長度，則有：

f[1][1]=same(1,1)

f[i][j]=max{f[i-1][j-1]+same(i,j),f[i-1][j],f[i][j-1]}

其中，same(a,b)當 X 的第 a 位與Y的第b位完全相同時為“1”，否則為“0”。

此時，f[i][j]中最大的數便是X和Y的最長公共子序列的長度，依據該數組回溯，便可找出最長公共子序列。

該演演算法的空間、時間複雜度均為O(n^2)，經過優化后，空間複雜度可為O(n)，時間複雜度為O(nlogn)。

代碼實現

pascal語言實現：

Pascal

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

constmaxlen=200;

var

i,j:longint;

c:array[0..maxlen,0..maxlen]ofbyte;

x,y,z:string;{z為x,y的最長公共子序列}

begin

readln(x);

readln(y);

fillchar(c,sizeof(c),0);

fori:=1tolength(x)do

forj:=1tolength(y)do

ifx[i]=y[j]thenc[i,j]:=c[i-1,j-1]+1

elseifc[i-1,j]>c[i,j-1]thenc[i,j]:=c[i-1,j]

elsec[i,j]:=c[i,j-1];

z:='';

i:=length(x);

j:=length(y);

writeln(c[i,j]);

while(i>0)and(j>0)do

ifx[i]=y[j]

thenbeginz:=x[i]+z;i:=i-1;j:=j-1end

elseifc[i-1,j]>c[i,j-1]theni:=i-1

elsej:=j-1;

ifz<>''thenwriteln(z);

fori:=1tolength(x)do

begin

forj:=1tolength(y)dowrite(c[i][j]:3);

writeln;

end;

readln;

end.

C++語言實現：

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

#include

const int lcs__xy=100001;

int lcs__dp[2][lcs__xy];

long long bigger(long long x,long long y)

{

return x>y?x:y;

}

templateint lcs(kind *x,kind *y,int l1,int r1,int l2,int r2,bool(*equality)(kind,kind))

{

if(l1>r1)return 0;

int num=(r2+1)*sizeof(kind);

memset(lcs__dp[0],0,num);

for(int i=l2;i<=r2;i++)

if(x[l1]==y[i])

{

for(;i<=r2;i++)lcs__dp[0][i]=1;

break;

}

for(int i=++l1,j;i<=r1;i++)

{

for(j=l2;j<=r2;j++)

{

if(equality(x[i],y[j]))lcs__dp[1][j]=lcs__dp[0][j-1]+1;

else lcs__dp[1][j]=bigger(lcs__dp[0][j],lcs__dp[1][j-1]);

}

memcpy(lcs__dp[0],lcs__dp[1],num);

}

return lcs__dp[0][r2];

}

目錄