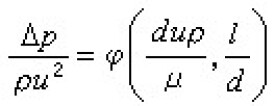因次分析
因次分析
又稱量綱分析,量綱分析的基礎是量綱一致性的原則和所謂的π定理。量綱一致性的原理表明:凡是根據基本物理規律導出的物理方程,其中的量綱必然相同。根據白金漢(Buckingham)所提出的π定理,任何量綱一致的物理方程都可以表示為一組量綱為1數群的零函數,即:F(π1,π2,π3,...,πi)=0。
是對過程有關物理量的因次(即量綱)進行分析,得到為數較少的無因次數(即無量綱參數)群間關係的方法,和相似論方法同為指導實驗的化學工程研究方法,在工程學科的研究中有著廣泛的應用。
①很多物理量都是有因次的,如速度的因次為(長度/時間),寫作LT-1,密度的因次為(質量/長度3),寫作ML-3等。若干物理量總能以適當的冪次組合構成無因次的數群,如在研究管內流動時,可將速度 u、管徑d、流體密度ρ,流體粘度μ 四個量組成一個無因次數群,即雷諾數Re。②任何物理方程總是齊因次的,即相加或相減的各項都有相同的因次。因此原則上,經過適當的變換,物理方程總可以改寫為無因次數群間關係的形式。
π定理 π定理是由任何物理方程都是齊因次的這一事實推出的。此定理指出:對一特定的物理現象,由因次分析得到無因次數群的數目,必等於該現象所涉及的物理量數目與該學科領域中基本因次數之差。例如,在研究流體在光滑水平直管中作定態流動的流動阻力時,根據對這一物理現象的了解,已經知道壓力損失Δp與管徑d、管長l、流速u、流體密度ρ、流體粘度μ有關,這種關係可用如下函數表示:
該物理現象共涉及六個物理量。在力學中基本因次通常為長度、時間和質量,因而根據π定理可將式(1)變成三個無因次數群間的關係:
式中為歐拉數;為簡單幾何數群。這樣在實驗研究中便不需要測定各個物理量之間的定量關係,而只需測定上述無因次數群間的函數關係。
這種方法有兩個優點:①變數數減少了,實驗工作量可以減少;②由於只需逐次改變無因次數群的值,而不必逐個改變各物理量的值,實驗工作可以大大簡化。例如,在上述關於流動阻力的研究中,為改變雷諾數()的值,原則上只需改變流速u,既不需改變管徑d,也不需更換流體以改變流體性質ρ和μ,所得實驗結果可同樣有效地用於其他管徑和其他流體。
與相似論相比,因次分析方法不需要先列出描述過程的微分方程式,只需事先確定有關物理量。因此,因次分析方法的應用範圍較相似論廣。但是因次分析方法並不能指出哪些物理量是有關的和必要的,若過多地引入了一些關係不大的物理量,常常會增加分析上的複雜性;若遺漏了實際上有關的物理量(特別是當過程涉及無因次的物理量時),則可能導致嚴重的失誤。