四次方
四個相同的數相乘的數學術語
四次方是指4個一樣的數相乘,是一個數學術語,比如說,4x4x4x4的得數是4的四次方。
四次方的相反是四次方根,可以用平方根的平方根來計算。
在算術和代數中,數n的四次方是n的四個一樣的數相乘的結果。所以: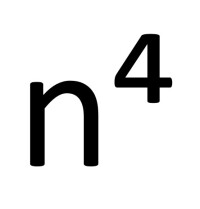 =n×n×n×n。
=n×n×n×n。
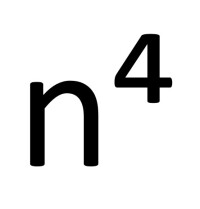
n的四次方
四次方也是通過將數字乘以它的立方(三次方)形成的。
整數的四次方的序列(也稱為雙重平方或tesseractic數)可以寫成:
0,1,16,81,256,625,1296,2401,4096,6561,10000,14641,20736,28561,38416,50625,65536,83521,104976,130321,160000,194481,234256,279841,331776,390625,456976,531441,614656,707281,810000,……
四次方寫作:^4,*&sup4。還有一種寫法,是在一個數的右上角寫一個小四,比如2的四次方寫作:2。
可以很容易地顯示基數為10中的整數的四次方的最後兩個數字(例如,通過計算可能的最後兩位數字的平方數的平方),這僅僅有十二種可能:
(1)如果一個數字以0結尾,則其四次方將以0結尾。
(2)如果一個數字以1,3,7或9結尾,其四次方以1,21,41,61或81結尾。
(3)如果一個數字以2,4,6或8號結尾,它的四次方將以16,36,56,76或96結尾。
(4)如果一個數字以5的形式結束,它的四次方以25結尾。(實際上以0625中結尾)。
這十二種可能可以方便地表示為0,h1,o6或25,其中o是奇數,h是偶數。
每個正整數可以表示為最多19個四次方的總和;每個足夠大的整數可以表示為最多16個四次方的總和。(參見[Waring'sproblem])。
Elkies表明,指數為4的其他反例是無窮多的,其中一些是:

例1
還有一些如下式:
由費馬公式可知,方程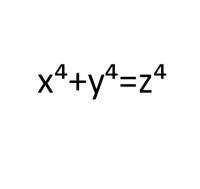 在非零整數(費馬的最後定理的特殊情況)中沒有解(見費馬的直角三角定理)。
在非零整數(費馬的最後定理的特殊情況)中沒有解(見費馬的直角三角定理)。
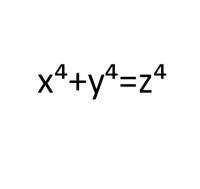
例4
阿基米德發現並證明了指數的規律,。在9世紀,波斯數學家穆罕默德·本·穆罕默德·哈維里姆(Muhammad ibnMūsāal-Khwārizmī)使用mal這個詞來代替平方,用kanb來代替立方,後來伊斯蘭數學家在數學符號中代表了m和k。
在16世紀末期,JostBürgi以羅馬數字為指數。
在17世紀初,我們現代指數符號的第一種形式是由Rene Descartes在他的文本“LaGéométrie”中引入的。在那裡,在第一冊中引入了符號。
Nicolas Chuquet在十五世紀使用了一種指數符號的形式,後來被Henricus Grammateus和Michael Stifel在16世紀使用。“指數”一詞在1544年由邁克爾·斯蒂夫創造。塞繆爾·傑克(Samuel Jeake)在1696年介紹了指數。在16世紀,羅伯特·史密斯(Robert Recorde)使用了平方(square),立方(cube),四次方(fourth power),五次方(fifth power),六次方(sixth power)。