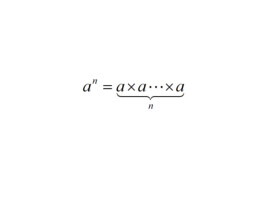指數

指數是冪運算aⁿ(a≠0)中的一個參數，a為底數，n為指數，指數位於底數的右上角。

當指數時，

當指數，且n為整數時，

當指數時，

當指數時，稱為平方

當指數時，稱為立方

冪運算（指數運算）是一種關於冪的數學運算。同底數冪相乘，底數不變，指數相加；同底數冪相除，底數不變，指數相減。冪的冪，底數不變，指數相乘。下面a≠0。

1）

2）

3）

4）

5）

如果，即的次方等於(且)，那麼數叫做以為底的對數，記作

其中，叫做對數的底數，叫做真數，叫做叫做“以 為底 的對數”。由此可見，在某種情況下（底數0，且不為1），指數運算中的指數可以通過對數運算求解得到。

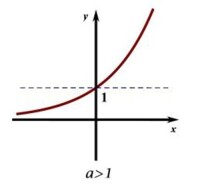
一般地，形如(且)()的函數叫做指數函數(exponentialfunction)，也就是說以指數為自變數，底數為大於0且不等於1的常量的函數稱為指數函數，它是初等函數中的一種。

指數函數圖像如下圖所示

曾經有人問愛因斯坦，世界上什麼事情最可怕？愛因斯坦說：“複利最可怕。”

複利就是將本金按一定利息存入銀行，到期將利息計入本金繼續存入銀行，本利不斷增加。如果本金為，年利息率為，年後可以從銀行取出的錢為。一般年利率 不會超過15%，而指數項，即存入銀行的年限 卻增長很快，當 足夠大時，本利相加會達到極其大的值。紐約曼哈頓地區是早期移民以價值200美元的珠寶從印地安人手中買下的，如果當初將200美元存入銀行，至今本息比曼哈頓的全部房產價值還要高。如果存入銀行1000元，年利率5%，若計複利的話，那麼200年後的便可以從銀行取到 元，即 元。

傳說在古印度有位國王要賞賜一位宰相，就問宰相想要什麼，宰相拿出一張國際象棋的棋盤。笑著說，我只求您給我一些麥粒，在第一個格子里放一粒（ ），第二格子里放兩粒（ ），第三個格子里放四粒（ ），也就是第 個格子里放 粒，直到每個格子的麥粒放好．國王以為這太簡單了，就爽快地答應了。可是等到真要執行這個諾言時國王卻不得不反悔了．這是為什麼呢？國際象棋棋盤共有64個格，按宰相的要求總共需要的麥粒數為等比數列 的和，即為 粒。若1公斤麥粒5萬粒，那麼總共需要的麥粒為 噸。這些麥粒也許把全國的麥子全拿來都不夠，國王怎麼可能答應呢？

不管是複利的可怕還是宰相的狡猾，都是因為其中含有共同的關鍵因素——指數項 ，是指數項 的奇妙作用，使得看似簡單的事情令人吃驚。

指數與冪的概念的形成是相當曲折和緩慢的指數符號(Signofpower)的種類繁多，且記法多樣化。

我國古代“冪”字至少有十各不同的寫法。

劉徽為《九章算術》作注，在《方田》章求矩形面積法則中寫道：“此積謂田冪，凡廣從相乘謂之冪(長和寬相乘的積叫作冪)。”這是第一次在數學文獻上出現冪。

《准南子·天文訓》講到樂律，有這樣幾句話：“故黃鐘之律九寸，而宮音調；因而九之，九九八十一，故黃鐘之有選舉權立焉......十二各以三成，故置一而十一三之，為積分十七萬七千一百四十七，黃鐘大數立焉。”可翻譯如下：發出黃鐘音律的管長9寸，它的音調叫作宮。用9去乘它得81。81這個數叫作黃鐘數。12律的每一個是根據三分損益這個原則造成的。所以將3乘了11次，得到的積，分管長177147等份，這177147叫作黃鐘大數，以別於黃鐘數81。很明顯，“置一而十一三之”就是乘方運算，11就是現在的指數。整句話包含式子，具有指數的初步概念。

1607年，利瑪竇和徐光啟合譯歐幾里得的《幾何原本》，在譯本中徐光啟重新使用了冪字，並有註解：“自乘之數曰冪。”這是第一次給冪這個概念下定義。

至十七世紀，具有“現代”意義的指數符號才出現。最初的，只是表示未知數之次數，但並無出現未知量符號。比爾吉則把羅馬數字寫於係數數字之上，以表示未知量次數。其後，開普勒等亦採用了這符號。羅曼斯開始寫出未知量的字母。1631年，哈里奧特(aa表示以aaa表示。1636年，居於巴黎的蘇格蘭人休姆(JamesHume)以小羅馬數字放於字母之右上角的方式表達指數，如以表示，該表示方式除了用的是羅馬數字外，已與指數表示法相同。笛卡兒(1596-1650)以較小的印度阿拉伯數字放於右上角來表示指數，是現今通用的指數表示法。