角動量
與物體到原點的位移和動量相關的物理量
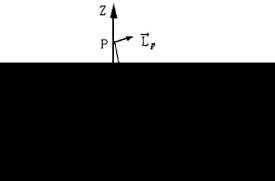
質點動量p對O點之動量矩(通常稱為角動量)L(O)(簡記為L)為
L=r×p
其中r是質點相對O點的位矢(位置矢量)。
角動量L的大小為L=rpsinφ(φ為r與p的夾角),方向垂直於位矢r和動量p所組成的平面,指向是由r經小於180°的角轉到p的右手螺旋前進的方向。
角動量在物理學中是與物體到原點的位移和動量相關的物理量。在經典力學中可被定義為物體到原點的位移(矢徑)和其動量的叉積:
角動量
角動量
角動量
角動量
角動量
其中,r表示以質點到旋轉中心(軸心)的距離(標量值可以理解為半徑的大小),方向由原點指向物體位置的矢量(即矢徑),L 表示角動量,v表示線速度,P表示動量,表示轉動慣量,表示角速度(矢量)。角動量是矢量,且是軸矢量。其量綱為,SI單位制中單位為。
角動量的方向:角動量是兩個矢量的叉乘,在右手坐標系里遵循右手螺旋法則,即右手四指指向矢徑的方向,轉過一個小於180度的平面角后四指指向動量的方向,則大拇指所指的方向為角動量的方向。
角動量與轉動慣量的關係
對於定軸轉動的剛體,在常見的情況下(不是所有情況,見註記7),
角動量
角動量
角動量
角動量
角動量
是轉動慣量(SI 單位為),是角速度(矢量)(SI 單位為)。
角動量守恆定律稱,在不受外力矩作用時,體系的總角動量不變。
注意角動量守恆是矢量守恆,這代表其三個分量都不隨時間而變化。
體系受到外力矩作用時,有
角動量
角動量
1、角動量是描述物體轉動狀態的量。又稱動量矩。
2、角動量是矢量,它在通過O 點的某一軸上的投影就是質點對該軸的角動量(標量)。
3、質點系或剛體對某點(或某軸)的角動量等於其中各質點的動量對該點(或該軸)之矩的矢量(或代數)和。
4、角動量的幾何意義是矢徑掃過的面積速度的二倍乘以質量。角動量守恆定律指出在合外力矩為零時,物體與中心點的連線單位時間掃過的面積不變,在天體運動中表現為開普勒第二定律。
5、角動量在量子力學中與角度是一對共軛物理量。
6、角動量是剛體動力學中與動量對應的概念,它的大小取決於轉動的速率和轉動物體的質量分佈。
7、在常見的情況下,角動量和角速度方向相同,但更一般地來講,二者的方向不必相同,甚至在剛體作定軸轉動的情況下也是如此(利用向量的三重矢積運演演算法則可證,此略)。