質點

質點就是有質量但不存在體積與形狀的點。通常情況下如果物體大小相對研究對象較小或影響不大，可以把物體看做質點。

質點 mass point，物理學專有名詞。不考慮物體本身的形狀和大小，並把質量看作集中在一點時，就將這種物體看成“質點”。研究問題時用質點代替物體，可不考慮物體上各點之間運動狀態的差別。它是力學中經過科學抽象得到的概念，是一個理想模型。可看成質點的物體往往並不很小，因此不能把它和微觀粒子如電子等混同起來。若研究的問題不涉及轉動或物體的大小跟問題中所涉及到的距離相比較很微小時，即可將這個實際的物體抽象為質點。例如，在研究地球公轉時，地球半徑比日、地間的距離小得多，就可把地球看作質點，但研究地球自轉時就不能把它當成質點。又如物體在平動時，內部各處的運動情況都相同，就可把它看成質點。所以物體是否被視為質點，完全決定於所研究問題的性質。

質點是將物體簡化后得到的只有質量而不計大小、形狀的一個幾何點，是經典力學中常用的最基本的模型。作平動（見機械運動）的物體，不論其大小、形狀如何，體內任一點的位移，速度和加速度都相同，可以用其質心這個點的運動來概括，即可視為質點的運動。

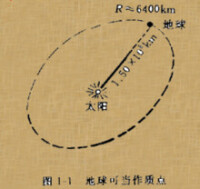
在地球繞太陽的公轉中，球中任一點對太陽的位移、速度和加速度都略有差別，但地球半徑遠小於地球太陽間的距離，上述差別也遠小於地心的位移、速度和加速度，可以忽略不計，仍可視公轉為質點運動。在物體的轉動例如地球的自轉中，球內各點的位移、速度和加速度的方向及大小差別懸殊，完全不能忽略，就不能視為質點。但可把物體無限分割為極小的質元，每個質元都可視為質點，物體的轉動就成為無限個質點的運動的總和，即質點系的運動。

另一方面，從物體所受引力的角度來看，如果物體的尺寸遠較它和產生引力場的另一物體間的距離為小時，可以忽略其形狀、尺寸，視為質點；相近時，就須視為質點系。所以世界上一切物體的機械運動均可視為質點或質點系的運動，而質點運動學和質點系動力學也就成了經典力學的基礎。

若一質點的質量為M1，位於軸上的點P1處，P1的坐標為X1；一質點的質量為M2，位於軸上的點P2處，P 2的坐標為X2，則這兩個質點所形成的質點系重心P的坐標X=（M1X1+M2X2）/（M1+M2）

如果你僅僅是要描述一個物體運動的特點（對外界運動，其自身的狀態如何改變都不會影響運動）就可以當作質點.

這樣比喻：

如果有一輛火車要從廈門開往北京的話

那在地圖上就可以當做質點（因為就算那個火車是圓的或者是方的對你所要描述的都沒有影響）

而當你要描述這輛火車完全經過100米時的運動時你就不能把它當成一個質點..因為它有車身的長度，而這個長度會改變它的運動特點（例如要把車尾也算在內）這樣它就不能當作是質點了。

如果你要研究一個原地旋轉的球，他也不能被當做質點。因為如果看成質點，就不能探究他的旋轉了

在一個選定的參考系中，當質點運動時，它的位置P（x,y,z）是按一定規律隨時刻t而改變的，所以位置是t的函數，這個函數可表示為：

x=x(t) ,y=y(t),z=z(t)

它們叫做質點的運動學方程（kinematical equation）。

在坐標系中，質點的位置常用位置矢量（position vector ,簡稱位矢）位矢是從原點指向指點所在位置的有向線段，用矢量r表示。

彼此有相互作用的許多質點構成的力學系統叫質點組，也叫質點系。

1.質點組必須彼此有相互作用。(一群毫無相聯繫的蚊蠅以及一盤散沙，都不是質點組)

2.質點組之間的內力與外力：內力記為F(i)，外力記為 F(e)。性質：質點組中各內力的矢量和恆為零。

3. 質點組動量定理與守恆律：它是剛體力學的基礎之一。

一 質點組動量定理 質點組的動量的變化率等於質點組所受外力的矢量和。

二質心運動定理質點系質量與質心加速度的乘積總是等於質點系所受一切外力的矢量和。

三 質點組動量守恆律 若質點組受的外力矢量和為零，則質點組動量P=恆量。

質點組動量守恆定律表明：若 ΣFi(e)=0，則P=Pc=恆量，即質心作勻速直線運動(Vc=恆量)，內力不會引起質心運動狀態的改變。

4.質點組動量矩定理與動量矩守恆律

5.質點的基本屬性：只佔有位置而不佔空間，具有被代替物質的全部質量。

一 質點組對定點O的動量矩定矩定理。質點組對定點的動量矩的時間變化率等於受到的外力矩。

二 對質心的質點組動量矩定理 1、質心坐標系 設oxyz為靜止系，若另一坐標系cx'y'z'隨質點組運動而運動，原點取在質點組的質心，坐標軸與基本系oxyz的坐標軸平行，則cx'y'z'叫質心坐標系. 質心坐標系的特點是：在質心繫中，質心的位置矢量 rc=0

2、對質心繫的動量矩定理 dJ'/dt=M' 該式表明：對質心的動量矩J'的對時間的變化率等於作用於質點組的外力對質心的力矩(該式稱為對質心的動量矩定理)。此式還表明了質心繫的特殊性：質心繫一般情況而言並不是慣性系，但是，質心繫中的質點組動量矩定理仍保持與慣性系中相同的形式。此式還表明：慣性力、內力對質心的力矩恆為零。

3.質點組動能定理與機械能守恆律

一 質點組動能定理和機械能守恆律 質點組動能的變化等於質點組受的外力和內力作功之和(動能定理)。顯然：只有當運動時兩質點間距離保持不變(如剛體)，內力作功才為零。一般情況內力作功不為零。特例：若外力、內力都是保守力，則質點組的機械能守恆。

二 對質心的動能定理 質點組對質心繫的動能的變化等於外力和內力對質心繫作功之和。

三柯尼希定理：質點系的總動能等於全部質量集中在質心時質心的動能，加上各質點相對於質心平動坐標系運動所具有的動能。

質點定義是經典物理最早期的科學定義，它只考慮了物體的質量而沒有考慮物體的內在電荷，致使以質點定義為基礎的經典力學體系無法與電磁學，電動力學，狹義相對論及現代物理完全兼容。

現代物理證明，任何物體的最終物質組成都是電子（帶單位負電），質子（含有兩個帶2/3電荷的u夸克和一個帶-1/3電荷的d夸克）和中子（含有兩個d夸克和一個u夸克）等三種基本粒子。儘管由它們所組成的原子，分子或物體多為電中性，但其內部電荷組成不容忽視。

例如當研究運動的氫原子時，如果將氫原子抽象為質點，則只能與經典力學相聯繫。如果將其視為電子圍繞著原子核運動，則與電磁學，電動力學，原子物理，以及量子力學相聯繫。

具有一定質量而不計大小尺寸的物體。物體本身實際上都有一定的大小尺寸，但是，若某物體的大小尺寸同它到其他物體的距離相比，或同其他物體的大小尺寸相比是很小的，則該物體便可近似地看作是一個質點。例如行星的大小尺寸比行星間的距離小很多，行星便可視為質點-因為不計大小尺寸，所以質點在外力作用下只考慮其線運動。

由於質點無大小可言，作用在質點上的許多外力可以合成為一個力，另一方面，研究質點的運動，可以不考慮它的自旋運動。

任何物體可分割為許多質點，物體的各種複雜運動可看成許多質點運動的組合。因此，研究一個質點的運動是掌握各種物體形形色色運動的入門。牛頓第二定律是適合於一個質點的運動規律的。有了這個定律，再配合牛頓第三定律，就構成了研究有限大小的物體的手段。所以“質點”是研究物體運動的最簡單、最基本的對象。

用來代替物體的有質量而不考慮形狀和大小的點。是一個理想的模型，實際上並不存在。

天文學的雙星（多星）天體圍繞同一質點做環繞運動。（如冥王星-卡介，地球-月球，系外雙星星系）。

當研究地球繞太陽運動時，可以將地球看做質點，此時地球的大小形狀對所考慮的問題無明顯影響；而在研究地球與其衛星時，並不可以把地球看做質點，因為此時地球的大小形狀對所研究的問題影響顯著。

要把物體看作質點，就要看所研究問題的性質，而與物體本身無關。所以，能否將物體看作質點需要滿足其中之一：

當物體的大小與所研究的問題中其他距離相比為極小時。

一個物體各個部分的運動情況相同，它的任何一點的運動都可以代表整個物體的運動。

理想化條件下，滿足條件有：

（1）物體上所有點的運動情況都相同，可以把它看作一個質點。

（2）物體的大小和形狀對研究問題的影響很小，可以把它看作一個質點。

（3）轉動的物體，只要不研究其轉動且符合第2條，也可看成質點。

可視為質點的運動物體有以下兩種情況：

（1）運動物體的形狀和大小跟它所研究的問題相比可忽略不計，如研究地球繞太陽的公轉，可把地球當作一質點。

（2）做平動的物體，由於物體上各點的運動情況相同，可以用一個點代表整個物體的運動。

1、質點是一個理想化的模型﹐它是實際物體在一定條件下的科學抽象。

2、質點不一定是很小的物體﹐只要物體的形狀和大小在所研究的問題中屬於無關因素或次要因素﹐即物體的形狀和大小在所研究的問題中影響很小時﹐物體就能被看作質點。它注重的是在研究運動和受力時物體對系統的影響，忽略一些複雜但無關的因素。

3、在理論力學中，一個物體常常抽象為它的重心，尤其在靜力學和運動學中。

質點的基本屬性

1．只佔有位置，不佔有空間，也就是說它是一維的。

2．具有它所代替的物體的全部質量。