狹義相對論
需要使用引入張量的數學工具
狹義相對論（Special Theory of Relativity）是阿爾伯特·愛因斯坦在1905年發表的題為 《論動體的電動力學》一文中提出的區別於牛頓時空觀的新的平直時空理論。“狹義”表示它只適用於慣性參考系。這個理論的出發點是兩條基本假設：狹義相對性原理和光速不變原理。理論的核心方程式是洛倫茲變換（群）（見慣性系坐標變換）。狹義相對論預言了牛頓經典物理學所沒有的一些新效應（相對論效應），如時間膨脹、長度收縮、橫向多普勒效應、質速關係、質能關係等。狹義相對論已經成為現代物理理論的基礎之一：一切微觀物理理論（如基本粒子理論）和宏觀引力理論（如廣義相對論）都滿足狹義相對論的要求。這些相對論性的動力學理論已經被許多高精度實驗所證實。
狹徠義相對論不僅包括如時間膨脹等一系列推論，而且還包括麥克斯韋－赫茲方程變換等。狹義相對論需要使用引入張量的數學工具。
狹義相對論是對牛頓時空理論的拓展，要理解狹義相對論就必須理解四維時空，其數學形式為閔可夫斯基幾何空間。
現在對於物理理論新的分類標準，是以其理論是否是決定論來劃分經典與非經典的物理學，非量子理論都可以叫經典或古典理論。在此意義上，狹義相對論仍然是一種經典的理論。
《狹義相對論》
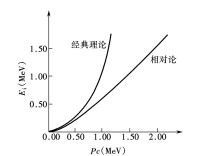
狹義相對論
①邁克耳孫－莫雷實驗沒有觀測到地球相對於以太的運動，同經典物理學理論的“絕對時空”和“以太”概念產生矛盾。
②運動物體的電磁感應現象表現出相對性——是磁體運動還是導體運動其效果一樣。
拓展牛頓理論使之能夠圓滿解釋上述新現象成為19世紀末、20世紀初的當務之急。以H.洛倫茲為代表的許多物理學家在牛頓力學的框架內通過引入各種假設來對牛頓理論進行修補，最後引導出了許多新的與實驗結果相符合的方程式，如時間變慢和長度收縮假說、質速關係式和質能關係式，甚至得到了洛倫茲變換。所有這些公式中全都包含了真空光速。如果只為解釋已有的新現象，上述這些公式已經足夠，但這些公式分別來自不同的假說或不同的模型而不是共同出自同一個物理理論。而且，使用牛頓絕對時空觀來對洛倫茲變換以及所含的真空光速進行解釋時卻遇到了概念上的困難。這種不協調的狀況預示著舊的物理觀念即將向新的物理觀念的轉變。愛因斯坦洞察到解決這種不協調狀況的關鍵是同時性的定義，同時性概念沒有絕對的意義。而牛頓時空理論（或伽利略變換）中的時間沒有辦法在現實世界中實現。為使用光信號對鍾，愛因斯坦假定了單向光速是個常數且與光源的運動無關（光速不變原理）。此外，他又把伽利略相對性原理直接推廣為狹義相對性原理，由此得到了洛倫茲變換，繼而建立了狹義相對論。
狹義相對性原理：一切物理定律（除引力外的力學定律、電磁學定律以及其他相互作用的動力學定律）在所有慣性系中均有效；或者說，一切物理定律（除引力外）的方程式在洛倫茲變換下保持形式不變。不同時間進行的實驗給出了同樣的物理定律，這正是相對性原理的實驗基礎。
光速不變原理：光在真空中總是以確定的速度c傳播，速度的大小同光源的運動狀態無關。在真空中的各個方向上，光信號傳播速度（即單向光速）的大小均相同（即光速各向同性）；光速同光源的運動狀態和觀察者所處的慣性系無關。這個原理同經典力學不相容。有了這個原理，才能夠準確地定義不同地點的同時性。
如果在某個慣性系中看來，不同空間點發生的兩個物理事件是同時的，那麼在相對於這一慣性系運動的其他慣性系中看來就不再是同時的（時間是一個坐標數據，某個坐標系中“時間維坐標”相同的兩個不同位置的點，在另一個坐標系“時間維坐標”不同是很正常的）。所以，在狹義相對論中，同時性的概念不再有絕對意義（坐標數據是沒有絕對的，相同的一個點在不同的坐標系中4個坐標數據完全可不相同），它同慣性系有關，只有相對意義。但是，對於同一空間點上發生的兩個事件，同時性仍有絕對意義（3維空間坐標相同的兩個不同時空點，仍然是兩個不同的時點；但是狹義相對論規定這兩個不同時空點的時間維距離是等效的，規定是有絕對意義的）。
使牛頓力學第一定律（慣性定律）成立的那類參考系稱為慣性系。狹義相對論的公式和結論只在慣性系中有效。兩個慣性系K和K'之間的坐標變換是洛倫茲變換：
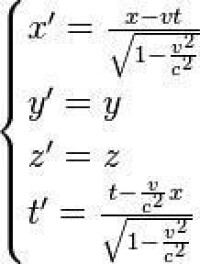
《狹義相對論》
式中（c就是一個單純的數學數據，假定三維空間中時鐘光子勻速直線運動1米，就是時間坐標數據“1秒/c”）為光在真空中傳播的速度，v為K'系相對於K系的速度。
洛倫茲變換是線性變換，把其中的時空坐標換成任意坐標間隔其形式不變。所以，洛倫茲變換中的時空坐標也可當成是任意坐標間隔，比如x,y,z 是在慣性系K中的移位，t是在慣性系K中的時間間隔，x‘,y’,z‘ 是在慣性系K’中的移位，t‘是在慣性系K’ 中的時間間隔。這裡K系和K'系被選成坐標軸互相平行且在初始時刻兩系統的坐標原點重合，因而這裡給出的變換是無空間轉動的特殊洛倫茲變換。更一般的變換是把K'系統的坐標軸相對於K系做一任意的空間轉動，相應的變換稱為一般洛倫茲變換。另外，如果在初始時刻不使兩系統的原點重合，則相應的變換就是在洛倫茲變換中每個公式的右邊各加上一個常數（稱為時空平移）使之成為非齊次的線性變換，它們稱為彭加勒變換。
洛倫茲變換是狹義相對論中最基本的關係式，反映了時間和空間是不可分割的，要確定一個事件，必須同時使用三個空間坐標和一個時間坐標，這四個坐標（數據）所組成的空間稱為四維空間（四維時空）。
在低速情況下，被觀察的物質的速度也遠比光速小，洛倫茲變換率約為“1"，退化為近似伽利略變換。相對論力學是由相對性原理（牛頓力學）和洛倫茲變換建立起來的，牛頓力學是狹義相對論的一種特殊形式（洛倫茲變換率約為“1"的情況下），在低速情況下狹義相對論性力學近似於牛頓力學。
因為時空坐標的洛倫茲變換率不同和參照時鐘的移動數據不同，所以合成速度不是簡單的數學加減。
如果洛倫茲變換中的時間坐標和空間坐標描述的是某一物體的運動，則用時間變換式去除3個空間坐標變換式就得到愛因斯坦速度相加公式（對洛倫茲變換的三個公式關於時間求一階導數）：
u'=(u－v)/(1－vu/c )
u'=u(1－v /c ) /(1－vu/c )
u'=u(1－v /c ) /(1－vu/c )
式中(u',u',u')為物體在K'系中的速度分別沿(x',y',z')軸的分量，(u,u,u)則為物體在K系中的相應速度分量，v則為K'系在K系中的速度，其中v應當為(v ,,)。此式為特殊洛倫茲速度變換，任意方向v變換請參考普遍洛倫茲變換。
愛因斯坦速度相加定理解釋了A.斐索曾於1851年完成的流動水中的光速實驗；1905年之後許多運動流體和運動固體中的光速實驗也都在更高的精度上與愛因斯坦速度相加公式的預言相符。
由同一隻標準時鐘記錄的時間（間隔）稱為固有時（間隔）；放在不同地點的兩隻標準時鐘記錄的時間之間的差值稱為坐標時（間隔）。物理時間（指實際直接測量的時間）對應於固有時；而坐標時與同時性定義相關，不是直接的可觀測量。這些是閔可夫斯基幾何的內容，想要深入了解的讀者，請翻閱劉遼教授，趙崢教授或梁燦彬教授關於相對論的著作！
由同一個光子在空間坐標系中勻速運動的直線為時間坐標軸刻度的時間坐標數據為固有時，獨立選擇光子在時空坐標系中勻速運動的直線為時間坐標軸刻度的時間坐標數據為固有時等效時，也稱坐標時。
狹義相對論預言（這不是預言，而是數學假設、數學邏輯的結果），運動時鐘的“指針”行走的速率比時鐘靜止時的速率慢，這就是時鐘變慢或時間膨脹效應。考慮在K系中的某一點靜止不動（即空間坐標間隔為零：x=0，y=0，z=0）的一隻標準時鐘，此時洛倫茲變換中的前三個方程給出：
x'=vt'，y'=0，z'=0
這是時鐘在K'系中的運動軌跡，即時鐘以不變速度v沿x'軸的正方向運動。洛倫茲變換中的第三個方程給出（如下圖）：
《狹義相對論》
相對論中，動能定理仍然成立，但動能形式有所不同，動量定義仍為質量與速度的乘積。質能關係大大拓展了人們對於質量和能量這兩個概念的認識，把質量的變化和能量的變化聯繫起來。兩者關係為：
核反應中所釋放的巨大能量，正是前後粒子質量的微小變化（虧損）的結果。原子彈和核反應堆就是根據這一原理製成的。儘管質能關係是愛因斯坦的一種假設，但已成為大量實踐所證實，它為人類開發利用能源提供了一條新途徑。
《狹義相對論》
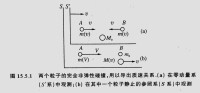
設在S'系中有一對全同粒子A,B沿x‘軸相向運動，速度均為v正碰后成為一個複合粒子，且靜止不動[圖15.5.1(a)]，設s’系以速度v沿同一直線相對S系運動，在S系中B靜止不動，粒子A以V速度運動，其速度V可由速度變換求得，為
（1）
剩餘推導過程如圖。
《狹義相對論》
質速關係部分推導1
《狹義相對論》
此式即為質速關係，它與實驗完全符合。
相對論中，動量定義仍為質量與速度的乘積。但質量是是速率的函數，於是動量
其實相對論動量的概念在上文導出質速關係時已經用到過。
相對論中，力被定義為動量的時間變化率，即
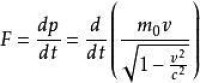
《狹義相對論》
相對論中，動能定理仍然成立，設F沿粒子方向施加於粒子。力的元功
部分推導如圖
《狹義相對論》
兩邊積分，得
若取初態v1=0，則Ek1=0，終態v2=v，對應動能Ek，其質量m(v)，則有
m0c^2與粒子處於靜止狀態的能量相對應，稱為粒子的靜能。m（v）^2為粒子處於運動狀態的能量，數值上等於Ek與靜能之和。愛因斯坦把m（v）c^2稱為粒子的總能量。Ek便是相對論能量。牛頓力學中的能量便是相對論能量在v<
時鐘變慢直接導致相對論性的多普勒效應（多普勒頻移）。當光源同觀察者之間有相對運動時，觀察者測到的光波頻率將同光源靜止時的光頻有差別，這種差別稱為多普勒頻移。經典理論也預言了多普勒頻移，但狹義相對論的預言同經典理論的預言不同（同一個數學結果，不同數學方法解題）。兩種預言之間的差別是由運動時鐘的速率不同於靜止時鐘的速率造成的，也就是時鐘變慢效應造成的。
光線的頻率和傳播的方向在洛倫茲變換下分別按如下公式變換：
ν'=(1－v·cosθ/c)(1－v /c )cosθ'=(cosθ－v/c)(1－v·cosθ/c)
式中ν和ν'分別為在K系和K'系中測得的光波頻率，θ和θ'為光線的傳播方向分別與x軸和x'軸的正方向之間的夾角。當θ=90°（即垂直於光線方向）時，
ν'=v/(1－v /c )
這就是橫向多普勒效應（牛頓經典物理學沒有這種效應）。橫向（或二階）多普勒效應實際上來自時間膨脹效應，它們已被很多實驗直接證實。
洛倫茲變換率假設
考慮放在K'系x'軸上的一根長桿，其長度稱為固有長度l≡x′。但在K系看來，這根杆子是運動的，運動杆子的長度定義為同時（即時間間隔t=0）測量杆子的兩端所獲得的空間坐標間隔。此時，洛倫茲變換給出：l≡x，運動杆子的長度變短了(l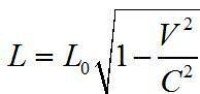
宇宙線μ子壽命的增長也可用長度收縮的觀點解釋。
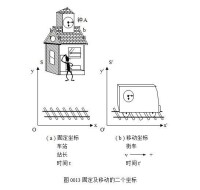相對論靠數學推演而成。本章主要以高中代數來推演狹義相對論。因數學比較難讀所以需要耐心。相對論是研究在速度不同的二個地方或坐標系內彼此時間及空間的關係。現在用車站及街車來做例子。圖 0013(a) 代表一個固定坐標的車站。站內的空間以x來代表水平方向位置，y來代表垂直位置，站上的鐘是 A ，時間是t。圖 0013(b) 代表一在移動坐標的街車，街車以速度v在水平方向離站。街車內的空間是以x'來代表水平方向位置，y'來代表垂直位置，車內的鐘是A'，時間是t'。
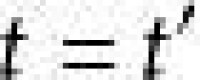0050
公式 0051 與 0052 中有四個係數D，E，F，及G，習慣以英文字母 來代表光速。為避免混亂，用c以後的中個字母來代表這四個新係數。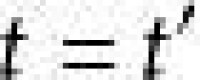
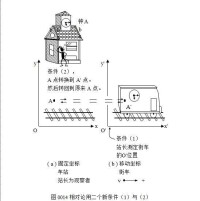圖0014顯示這兩個條件。圖0014（a）中有固定車站及站長。圖0014（b）中有街車，以速度v離開站。
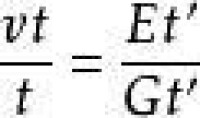0057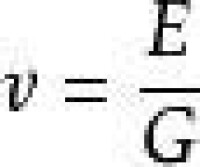
0058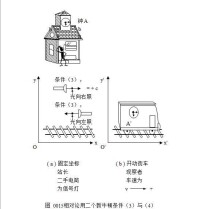
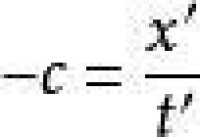
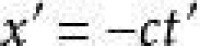街車裡人看到光是在
上二式中的變換方陣（matrix）是[ ] ,
x'及 為為開動中街車裡的位置及時間；
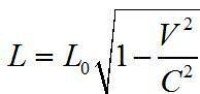
《狹義相對論》
牛頓力學在狹義相對論下的數學表達式：修改了速度數據，必須修正質量數據，才能保證F=ma；修改了質量數據，動量、動能數據註定要改寫。
按照狹義相對性原理，力學定律在洛倫茲變換下保持形式不變。為此，牛頓力學第二定律F=ma應當改寫為：
F=dp/dt，式中p=mu為物體的動量，u是速度。相對論力學中，物體的慣性質量分為靜質量m和相對論質量m，兩者的關係式稱為質速關係：
m與m兩者之差可以定義為動質量m=m－m狹義相對論預言，物體的慣性質量隨其運動速度的增加而加大，速度趨於光速時，慣性質量趨於無限大。
類似地，物體的能量分為固有能量E和相對論能量（總能量）E。動能K是總能與固有能量之差：K=E－E。能量與質量之間的關係式簡稱為質能關係，即：
E=mc
E=mc
動量、總能量、靜質量可組成下面的不變數（即在洛倫茲變換下保持不變）：
pc －E =－mc
在洛倫茲變換下動量p如同坐標矢徑r一樣變換，而能量E/c如同時間坐標ct一樣變換，即：
p'=1/(1－v /c ) (p－vE/c )
p'=p
p'=p
E'=1/(1－v /c ) (E－vp)
物理系統在一般洛倫茲變換下的不變性給出軌道角動量和自旋角動量守恆律；在時空平移變換下的不變性給出能量－動量守恆律。
洛倫茲變換率的假設，本身就已經假設了極限速度
由質能關係和質速關係可知，如果靜質量不為零的物體以光速c運動，則它的能量為無窮大。也就是說，把這樣的物體加速到光速需要做的功為無窮大，但這是不可能的。因此，通常物體的速度只能接近而不可能達到真空光速，即光速c是物質的極限速度。
光子在真空中的速度永遠是c，如果把它當成經典粒子，則由質速關係可知其靜質量必須是零；而且，一切以光速c運動的物質其靜質量也必定是零。在現實世界，通過大量的光學和電磁學的高精度實驗和分析，仍沒有發現光子有靜質量存在。
狹義相對論中，一維時間和三維空間構成閔可夫斯基四維平直時空，其度規可取為g=(－1,1,1,1)，任意兩個物理事件的四維間隔的平方寫為：
(Δs) =－c (Δt) +(Δx) +(Δy) +(Δz)
四維間隔的平方只有三種類型：(Δs) <0稱為類時間隔；(Δs) =0是類光間隔；(Δs) >0是類空間隔。相應的物理事件分別稱為類時事件、類光事件、類空事件。如果兩個物理事件代表的是某一物質的運動，它們分別是亞光速運動、光速運動、超光速運動。四維間隔在洛倫茲變換下保持不變，因而這三類不同類型的運動不會通過坐標變換而互相轉化。如亞光速運動不可能變為超光速運動；反之亦然。
按照狹義相對論，靜質量為正實數的通常物質其運動速度一定小於光速c，這類物質稱為亞光速物質（或亞光速粒子），它們的全體稱為亞光速世界。狹義相對論也允許超光速世界的存在，其中所有物質的速度都超過光速c，這類物質（或粒子）稱為快子，其靜質量是虛數（其平方小於零）。物理學家曾經設計過許多實驗，但都沒有發現快子的蹤跡。如果在亞光速世界里能夠出現快子，就會有違反因果律的現象發生：考慮在某一給定慣性系中的第一點發生了第一個物理事件，同時有一個超光速信號把這個信息傳送到第二點而觸發了第二個事件，我們說這兩個事件具有因果聯繫且滿足因果律：“原因”（第一個事件）在“結果”（第二個事件）之前發生。但按照洛倫茲變換，總能找到另外一些慣性系，在這些慣性系中“結果”（第二個事件）是在“原因”（第一個事件）之前出現的。因此，在狹義相對論中因果律排除了超光速信號的存在。
考慮三個慣性系K、K'、K''，其中K、K'的坐標軸互相平行因而它們之間是無轉動的洛倫茲變換；類似地，K、K''的坐標軸也互相平行因而它們之間也是無轉動的洛倫茲變換。但是，K'、K''之間則是有轉動的洛倫茲變換，即K''和K的坐標軸不再互相平行而是存在一個空間轉動，這種轉動稱為維格納轉動（經典物理學中的伽利略變換沒有這類效應）。1927年L.托馬斯首先把這種運動學效應應用於電子在原子核電場中作閉合軌道運動的情況，發現電子的磁矩在運動中會產生進動，這種進動後來被稱為托馬斯進動。考慮了托馬斯進動之後，原子光譜的精細結構分裂和反常塞曼效應就可同時得到圓滿解釋。托馬斯進動效應還表現在電子和μ子在均勻磁場中做圓周運動時其自旋的進動頻率：
ω=[(g－2)/2]eB/(mc)+ω
式中(g－2)因子相應於反常磁矩，e為電荷，m為靜質量，B為磁感應強度，c為光速，ω=eB/(γmc)是圓周運動的迴旋頻率，其中：
γ=1/(1－v /c )
多年來進行的電子和μ子的(g－2)因子的實驗測量結果與上面的理論預言在極高精度上相符合。
時間膨脹效應表明，運動時，鐘的速率將變慢。由於慣性系之間沒有哪一個更特殊，對於K和K'這兩個彼此作相對運動的慣性系來說，哪一個在運動，這完全是相對的。因而，似乎出現了這樣一個問題：K系中的觀察者認為K'系中的時鐘變慢了，而K'系中的觀察者又會認為K系中的時鐘變慢了，即兩個觀察者得到的是互相矛盾的結論。這就是所謂的“時鐘佯謬”問題。
如果把這個問題應用於假想的宇宙航行，就會給出這樣一個結果：有兩個孿生子，一個乘高速飛船到遠方宇宙空間去旅行，另一個則留在地球上。經過若干年，飛船重新返回到地球之後，地球上的那個孿生子認為乘飛船航行的孿生兄弟比他年輕；而從飛船上那個孿生子的觀點看，又好像地球上的孿生兄弟年輕了。這顯然是互相矛盾的。所以，這種現象通常又稱為“孿生子佯謬”或“孿生子悖論”。
在解釋這種佯謬時候，為了突出問題的實質，可以這樣來比較兩隻鍾，一隻鍾固定在一個慣性系中，另一隻鍾則相對於這個慣性系作往返航行，如同在“孿生子佯謬”中乘宇宙飛船的孿生兄弟那樣。通過研究在往返航行的鐘回來的時候，它的指針所顯示的經歷時間（也就是這個鐘所經歷的固有時間間隔）和固定鐘的指針所顯示的經歷時間（也就是固定鍾所經歷的固有時間間隔）相比，到底哪一個更長。顯然，經歷的固有時間間隔小的鐘，相當於年齡增長慢的那一個孿生子。可以發現，不能簡單地套用前面寫出的那個洛倫茲變換，因為往返航行的鐘並不是始終靜止於同一個慣性系之中，而是先靜止在一個慣性系（向遠處飛去），後來又經歷加速（或減速）轉而靜止在另一個慣性系（遠處歸來），而它的“孿生兄弟”即另外那一隻鍾則始終靜止在一個慣性系中。由此可見，往返航行的鐘和靜止的鐘的地位並不是等價的。其深層原因是兩個孿生兄弟在閔可夫斯基時空圖中的世界線是不相同的，這就反駁了“孿生子佯謬”。
具體地說，哪一隻走得更慢一些，有人認為，要解決這個問題，必須應用廣義相對論，因為有加速或減速過程。但是，實際上這個問題可以在狹義相對論範圍內圓滿解決。如果加速過程對時鐘速率不產生影響（實驗證明加速或減速過程對時鐘的速率沒有影響），考慮到作往返運動的時鐘經歷了不同的慣性系，因而還必須考慮到不同地點的同時性問題，那麼，不論在哪個慣性系中計算，狹義相對論都給出同樣的結果，即往返航行的時鐘變慢了。也就是說，在“孿生子佯謬”問題中，宇宙航行的孿生子比留在地球上的孿生兄弟年輕。
關於雙生子悖論也不必要如此麻煩，這裡告訴讀者一個很簡單的方法，同樣還是運用閔氏幾何，做出相應的圖像，很容易得到正確的說法，同樣可以參考上面提到的三位教授的書。
驗證狹義相對論的實驗大體上分為六大類：
①相對性原理的實驗檢驗
②光速不變原理的實驗檢驗
③時間膨脹實驗
④緩慢運動媒質的電磁現象實驗
⑤相對論力學實驗
⑥光子靜止質量上限的實驗
關於相對性原理的實驗檢驗，電動力學和光學的很多例子，特別是運動物體的電磁感應現象，都是很有說服力的，不再贅述，著重說明其餘五大類的驗證實驗。
首先，同光速不變原理有關的大量實驗已經證明，真空中光速同光源的運動速度和慣性運動狀態無關。定量的測量表明，真空中平均迴路光速с是一個常數，約為每秒30萬千米（с的精確測量值見基本物理常數）。這類實驗中，最著名的是邁克耳孫－莫雷實驗。這個實驗是在相對論出現之前很久的1881年首先由A.邁克耳孫完成的。1887年邁克耳孫和E.莫雷又用干涉儀以更高的精度重新做了觀測。這個實驗的目的是測量地球相對於以太的運動速度。但實驗結果同以太論的預言相矛盾。狹義相對論建立之後，這個實驗就被看成是光速不變原理和狹義相對性原理以及否定以太論的重要實驗基礎。還要說明一點，現有的實驗（包括邁克耳孫－莫雷實驗）並沒有證明光速是否同方向無關。引入光速同方向無關的假定是為了定義不同地點的事件的同時性，在沒有其他方法確定這種同時性之前，光速是否同方向無關是無法用實驗判斷的。
多普勒頻移的觀測，最高精度已達到 0.5%；對介子壽命的觀測，精度約達0.4%；用原子鐘做的實驗精度較低，約10%。這些實驗的結果都同相對論的預言符合。
在原子鐘環球航行的實驗中，雖然飛機速度遠小於光速，但由於測量精度很高，仍然觀測到了時間膨脹的相對論效應。
觀測運動介質對光速影響的實驗主要是斐索類型的實驗。這個實驗最初是A.斐索在1851年完成的，證明了運動介質中的光速同靜止介質中的光速不同，而且其差異和愛因斯坦速度相加公式的預言相符。通常把這種現象稱為“斐索效應”。近年來做的這類實驗中，運動介質的運動方向包括了同光線方向垂直或成布儒斯特角等各種情況，其結果也都同狹義相對論速度相加公式的預言相符。
包括質速關係（慣性質量隨物體運動速度的變化）和質能關係（即E=mс 關係）。質速關係是用電子和質子做的，事實上各種高能質子加速器和電子加速器的設計建造都驗證了質速關係。質能關係主要是通過核反應來進行檢驗，精度達到了百萬分之三十五。荷電粒子的電磁偏轉實驗、回旋加速器的運轉、高速粒子飛行時間的測量、原子光譜精細結構分裂的解釋等都為質速關係提供了證據。原子能發電、原子彈和氫彈的實現都以質能關係為理論基礎。
除了上述六類主要的實驗外，還有其他形式的實驗。所有這些實驗都沒有觀察到同狹義相對論有什麼矛盾。此外，狹義相對論在相對論性量子力學、量子場論、粒子物理學、天文學、天體物理學、相對論性熱力學和相對論性統計力學等領域中的成功應用，也都為它的正確性提供了豐富的證據。
雖然狹義相對論在理論的邏輯結構和形式上是很完美的，在實驗上已有了非常牢固的基礎，但人們仍對它不斷深入進行研究：理論方面，探討它在新領域中的應用；實驗方面，使用新的觀測方法和提高了測量精度的方法，更精密地檢驗它的正確性。此外還有不少實驗試圖觀察超光速現象，但至今並沒有得到令人信服的結果。
狹義相對論的建立，對物理學起了巨大的推動作用，並且深入到量子力學的範圍，成為研究高速粒子不可缺少的理論，並取得了豐碩的成果。但是有兩個原則性的根本問題未能解決。第一個是定義慣性系引起的困難。由於否定了“絕對時空”，慣性參考系（慣性系）成了無法定義的概念。如果慣性系是指牛頓第二定律在其中成立的參考系，那麼只有在慣性系中牛頓第二定律才能成立，從而陷入“邏輯循環”，整個理論如同建築在沙灘之上。第二個是萬有引力引起的困難。萬有引力定律與“絕對時空”緊密相連，必須加以修正，但其在洛倫茲變換下不具有協變性，因此無法納入狹義相對論的框架。直至廣義相對論建立之後，問題才得以徹底解決。
愛因斯坦的哲學信念：整個自然界是統一的、和諧的。他吸取了D.休謨對先驗論、E.馬赫對“絕對時空”概念的批判成果。其中馬赫哲學對愛因斯坦影響最大。馬赫認為時間和空間的量度與物質運動有關，時空觀念是通過經驗形成的，“絕對時空”沒有經驗根據。馬赫據此對牛頓的“絕對時間”和“絕對空間”進行批判，否定“絕對時空”概念，並認為時間測量依賴於參考系。愛因斯坦從考察兩個在空間上分隔開的事件的“同時性”入手，否定了“同時性”的絕對性及其有關的“絕對時間”概念，從而也否定了“絕對空間”概念以及實質上被當作絕對空間的“以太”的存在。愛因斯坦認為不存在絕對靜止的參考系，麥克斯韋－洛倫茲的電動力學方程是正確的，物體在慣性系中運動定律不變的假設導致光速不變的概念。
相對論中的光速不變性可以從理論上由麥克斯韋方程組得出：c=1/(εμ) ，光速由真空介電常數ε與磁導率μ決定，是一個不變的常數，並且不依賴於參考系的選擇。光速不變原理是宇宙時空對稱性的體現。
狹義相對論不但可以解釋經典物理學所能解釋的全部物理現象，還可以解釋一些經典物理學所不能解釋的物理現象，並且預言了不少新的效應。它導致了光速是極限速度，導致了不同地點的同時性只有相對意義，預言了長度收縮和時鐘變慢，給出了愛因斯坦速度相加公式、質量隨速度變化的公式和質能關係。此外，按照狹義相對論，光子的靜止質量必須是零。
狹義相對論把力學和電磁學在運動學的基礎上統一起來，揭示了作為物質存在形式的空間和時間在本質上的統一性以及同物質運動的聯繫。狹義相對論的時空觀，通過H.閔可夫斯基的工作得到重大發展。閔可夫斯基於1907年提出了空時四維表述形式，即在通常的空間三個坐標以外，引進第四個以光速和時間的乘積為尺度的虛坐標，這樣就可以方便地用四維空間中的幾何圖形來表示事件（稱為“世界點”）及其變化過程（稱為“世界線”）。在閔可夫斯基空間中，原來三維空間的距離和時間的間隔兩者各自獨立的不變性雖然不再成立，但兩者的結合體仍然是不變的。因此，他把這一觀點稱為“絕對世界的假設”。
愛因斯坦根據狹義相對論導出質量和能量的相當性（等價性），即物體的質量（m）是它所含能量（E）的量度：E=mc （c為真空中的光速），這就加深並發展了物質和運動的不可分離性原理。揭示了質量和能量是等價的，在本質上是同一的，證明自然界之間存在深刻的內在聯繫和統一性。按照狹義相對論的四維表示，能量和動量結合成一個量，即“能量－動量矢量（張量）”，動量是這個四維張量的空間分量，能量則是它的時間分量。這樣，動量守恆定律和能量守恆定律就結合成一個統一的能量－動量守恆定律。
狹義相對論的提出給物理學帶來了革命性的變化，更新了人們的世界觀，為廣義相對論的誕生奠定了堅實的基礎，改變了人類對宇宙和自然的“常識性”觀念，提出了“同時性的相對性”、“四維時空”等全新的概念。
狹義相對論的創立不僅引起了物理學的變革，而且對現代哲學產生了深遠的影響。它提出的新的時空觀、物質觀和運動觀，極大的發展了科學的自然觀。
愛因斯坦是如何創立狹義相對論的，請看下面的內容：
早在16歲時，愛因斯坦就從書本上了解到光是以很快速度前進的電磁波，與此相聯繫，他非常想探討與光波有關的所謂以太的問題。
牛頓認為，發光體發射出的是以直線運動的微粒粒子流，粒子流衝擊視網膜就引起視覺。18世紀牛頓的微粒說佔了上風，到19世紀，卻是波動說佔了絕對優勢。這短歷史我在《見微知著》中寫的很詳細了。
以太學說發展，人們認為：波的傳播需要媒質，光在真空中傳播的媒質就是以太。與此同時，電磁學得到了蓬勃發展，經過麥克斯韋、赫茲等人的努力，形成了成熟的電磁現象的動力學理論——電動力學，並從理論與實踐上證明光就是一定頻率範圍內的電磁波，從而統一了光的波動理論與電磁理論。
電磁學的發展最初也是納入牛頓力學的框架，但在解釋運動物體的電磁過程時卻發現，與牛頓力學所遵從的相對性原理不一致。按照麥克斯韋理論，真空中電磁波的速度，也就是光的速度是一個恆量；然而按照牛頓力學的速度加法原理，不同慣性系的光速不同。也就是麥克斯韋與伽利略關於速度的說法明顯相悖！
愛因斯坦似乎就是那個將構建嶄新的物理學大廈的人。他認真研究了麥克斯韋電磁理論，特別是經過赫茲和洛倫茲發展和闡述的電動力學。愛因斯坦堅信電磁理論是完全正確的，但是有一個問題使他不安，這就是絕對參照系以太的存在。
相對性原理已經在力學中被廣泛證明，在電動力學中卻無法成立，對於物理學這兩個理論體系在邏輯上的不一致，愛因斯坦提出了懷疑。他認為，相對性原理應該普遍成立，因此電磁理論對於各個慣性系應該具有同樣的形式，但在這裡出現了光速的問題。
光速是不變的量還是可變的量，成為相對性原理是否普遍成立的首要問題。當時的物理學家一般都相信以太，也就是相信存在著絕對參照系，這是受到牛頓的絕對空間概念的影響。
19世紀末，馬赫在所著的《發展中的力學》中，批判了牛頓的絕對時空觀，這給愛因斯坦留下了深刻的印象。1905年5月的一天，愛因斯坦與一個朋友貝索討論這個已探索了十年的問題，貝索按照馬赫主義的觀點闡述了自己的看法，兩人討論了很久。我在《變化》在討論慣性的時候，也引述馬赫原理。所以馬赫這個對愛氏的啟發是很大的。
突然，愛因斯坦領悟到了什麼，回到家經過反覆思考，終於想明白了問題。第二天，他又來到貝索家，說：謝謝你，我的問題解決了。原來愛因斯坦想清楚了一件事：時間沒有絕對的定義，時間與光信號的速度有一種不可分割的聯繫。他找到了開鎖的鑰匙，經過五個星期的努力工作，愛因斯坦把狹義相對論呈現在人們面前。
1905年6月30日，德國《物理學年鑒》接受了愛因斯坦的論文《論動體的電動力學》，在同年9月的該刊上發表。這篇論文是關於狹義相對論的第一篇文章，它包含了狹義相對論的基本思想和基本內容。
愛因斯坦解決問題的出發點，是他堅信相對性原理。伽利略最早闡明過相對性原理的思想，但他沒有對時間和空間給出過明確的定義。
牛頓建立力學體系時也講了相對性思想，但又定義了絕對空間、絕對時間和絕對運動，在這個問題上他是矛盾的。而愛因斯坦大大發展了相對性原理，在他看來，根本不存在絕對靜止的空間，同樣不存在絕對同一的時間，所有時間和空間都是和運動的物體聯繫在一起的。
在這篇文章中，愛因斯坦沒有討論將光速不變作為基本原理的根據，他提出光速不變是一個大膽的假設，是從電磁理論和相對性原理的要求而提出來的。這篇文章是愛因斯坦多年來思考以太與電動力學問題的結果，他從同時的相對性這一點作為突破口，建立了全新的時間和空間理論，並在新的時空理論基礎上給動體的電動力學以完整的形式，以太不再是必要的，以太漂流是不存在的。
什麼是同時性的相對性？不同地方的兩個事件我們何以知道它是同時發生的呢？一般來說，我們會通過信號來確認。為了得知異地事件的同時性我們就得知道信號的傳遞速度，但如何測出這一速度呢？我們必須測出兩地的空間距離以及信號傳遞所需的時間，空間距離的測量很簡單，麻煩在於測量時間，我們必須假定兩地各有一隻已經對好了的鐘，從兩個鐘的讀數可以知道信號傳播的時間。但我們如何知道異地的鐘對好了呢？
答案是還需要一種信號。這個信號能否將鍾對好？如果按照先前的思路，它又需要一種新信號，這樣無窮後退，異地的同時性實際上無法確認。不過有一點是明確的，同時性必與一種信號相聯繫，否則我們說這兩件事同時發生是無意義的。
大家體會到這個概念的重要了嗎？我在上面的各種提問，其實已經夠深入了。
相對論認為，光速在所有慣性參考系中不變，它是物體運動的最大速度。由於相對論效應，運動物體的長度會變短，運動物體的時間膨脹。但由於日常生活中所遇到的問題，運動速度都是很低的（與光速相比），看不出相對論效應。
愛因斯坦在時空觀的徹底變革的基礎上建立了相對論力學，指出質量隨著速度的增加而增加，當速度接近光速時，質量趨於無窮大。他並且給出了著名的質能關係式：E=mc^2，質能關係式對後來發展的原子能事業起到了指導作用。以上就是愛氏狹義相對論的創立過程。
摘自獨立學者靈遁者科普書籍《變化》
1922年愛因斯坦被子請到日本作為 6 個星期的巡迴演說。在京都大學 ( KyotoUniversity ) 時，有一位哲學教授西田 ( K.Nishida ) 請愛因斯坦講他如何發現相對論。愛因斯坦就臨時多加了一項演說來回答西田的問題。愛因斯坦的演說當場都有日文翻譯。後來物理學家大野 ( Yoshimosa Oono) 將日文翻譯成英文，登在今日物理 ( Physics Today ) 期刊上 ( 見文獻10 ) 。下面二段是那次演說中狹義相對論的發現過程的摘要。
愛因斯坦說，當他在大學時曾讀到邁克耳孫與莫雷的實驗，知道以太的構想是不對的。但他深信麥克斯韋及洛倫茲的公式是對的。另外有菲佐 ( Fizeau ) 的實驗，證明光速是不變的，不受其他速度的影響。這與我們平常的加減法是不同，有了矛盾。為什麼會有這矛盾呢？愛因斯坦花了一年的時間，想了各種方法來解說這矛盾，但都沒有好的結果。
在瑞士伯爾尼（Bern）一個好天氣的日子裡，愛因斯坦去找朋友貝索 (M.Besso )討論這問題，他們用各種不同的觀點來討論。突然愛因斯坦清楚了這問題的關鍵所在：不同速度地方的時間是不一樣的，時間會因相對速度而改變。這是一新的觀念，可將這矛盾解開了。次日愛因斯坦見到了貝索說：“謝謝你，我已將這問題解決了。”貝索聽了覺得莫明其妙。五個星期後，狹義相對論就寫成了。
以上的摘要中有提到的幾位科學家的研究尚宜加以說明。邁克耳孫與莫雷的實驗在第三 3 章內已提到過。這實驗證明光速不受地球速度的影響，是一不變的常數。洛倫茲與菲茨傑拉德提出長度縮減的假說，來解釋邁克耳孫與莫雷的結果。
麥克斯韋在1873年發表了電磁學說的基本公式。這些公式到現在還是經常應用。他證明電磁波的速度可以從空間中電磁的電容率（permittivity = capacitance / meter）及磁導率（ permittivity = inductance / meter ）計算出來，而發現電磁波的速度與光速完全相同。有名的物理學家玻爾茲曼（ L.Botzman ）稱讚麥克斯韋的公式，他借用哥德（Goethe）的一句話：“這些文章與公式是 不是一位神寫的呢？”（見文獻 36 ，頁 963）。
菲佐在1859年測量流動液體中的光速，發現光速並不受流體速度的影響。光速是固定不變的。這是很費解的謎（見文獻 8 ，頁 891）。
愛因斯坦注意了這謎有 7 年之久。1905 年他終於把這謎解決了。解開的關鍵點在於時間是可以改變的，他想出數學公式代表不同時間。當他將這些公式解開后，發現解出公式里有不少奇妙的好結果。這是科學上一大傑作，並且對世界有很大的影響。
《狹義相對論》
這二個不同速度坐標空間與時間的彼此關係在數學上叫做變換公式(transformation equation )。傳統的變換公式又叫做伽利略( Galiean )或牛頓( Newton )的變換公式，是
0049
《狹義相對論》
牛頓的公式 0049 中有二個係數A與B，以前已用二個條件來決定，為A=1及B=v。公式 0050 表示時間在二不同的地區是一樣的。若按照牛頓公式 0049 及式 0050 ，則光速會因光源的速度而改變。例如光源以速度v 趨近觀察者，依照這二個公式，該觀察者所測到的光速應是c+v。但是根據西特爾及邁克耳孫與莫雷的實驗，不管光源的移動多快，光速仍是c，牛頓公式 0049 及 0050 不符合。
為要與實驗相符，愛因斯坦提出新的變換公式如下：
0051
0052
《狹義相對論》
《狹義相對論》
牛頓與愛因斯坦的變換公式有什麼不同呢？牛頓公式（0049）與愛因斯坦公式（0051）是一樣的，只是將二個係數用不同的字母來表示而已。主要的不同存在於牛頓公式（0050）與愛因斯坦公式（0052）之間。牛頓的時間在任何地方都有是一樣的。愛因斯坦公式（ 0052 ）表示，時間在有相對速度的地區之間是不同的。這是一關鍵步驟，愛因斯坦他的新公式（0052）是他的一大發明，震動了全世界。
四個係數D，E，F及G它需要有四個物條件才能解出。其中有二個條件( 1 )及 ( 2 ) 是與以前牛頓的二條件相同的。愛因斯坦根據光速是固定不變而想出二個新的條件（3）及（4）。這四個條件將說明如下。條件（1）及（2）與牛頓的二個條件相同。
《狹義相對論》
條件（1）：站長測定街車的移動坐標原點 O' 位置。
條件（2）：固定站內的一點 A 變換到開動中街車裡成為 A' 點。然後又變回固定站內，則必須回到原來的 A 點上，圖 0014 。不然 A點可隨便改到另一個位置，這是不合理的。
愛因斯坦的新條件（3）和（4）。
愛因斯坦根據光速不變，不受光源速度的影響，想出了二個新條件。圖 0014(a) 是固定車站，站里有二手電筒，為信號燈，一向右照，一向左照。圖 0014（b）為移動的街車，是以速度 +v向右開走，街車裡有觀察者，他們的速度與街車相同，是 +v。右方向定為（+），左方向定為負向（-）。條件可以任何次序應用。將用條件（1），（3），（4）及（2）的次序來解四個係數。
條件（1）：站長測定街車的移動坐標原點 O' 位置，圖 0014 。
在開始時刻，固定與移動坐標原點 O 及 O' 可在同位置。車開動后，站長看到街車離去站長測到街車 O' 點的位置x等於街車速度v乘上時間，即x=vt。
街車裡的人，他自己原點 O' 隨車而走，是不變的，所以經常x'= 0 。
站長看到街車原點 O' 是在
0053
街車裡的人看到 O' 點是在
0054
將公式（0053）與（0054）代入愛因斯坦公式（0051）中，有
0055
將公式（0054 ）代入愛因斯坦公式（ 0052）里，有
0056
將式（0055 ）除以式（0056 ），即等號左邊相除等於右邊相除。
《狹義相對論》
上式中t 及t' 都被抵消了，得到
《狹義相對論》
上式乘以G 然後左右邊交換，有
0059
所以條件（1）決定了E和G之間的關係。
《狹義相對論》
《狹義相對論》
條件（3）：如圖 0015 (a) 在站里的一手電筒向右以光速 + 照。在站里，光速是，或。在街車內的人看的光速不變，仍是，或。所以
站長看到光是在
0060
街車裡人看到光是在
0061
將公式（0060 ）及公式（0061）代入愛因斯坦公式 ( 0051) 內，得
0062
將式（0061）代入愛因斯坦公式（0052）內，有
0063
將式（0062）除以式（0063），得到
0064
上式中t及t'又相抵消了，有
0065
以 上式乘以上式，有
0066
將上式各項重新排列成為
0067
《狹義相對論》
條件（4）：圖 0015 (a) 在站里的一手電筒向左以光速 -c照不變。在站里光速是，或x=-ct。在街車內的人看到的光速不變，仍是 或x'=-ct'。
除了光的方向改為左以外，條件（4）與（3）是一樣的。所以
站長看到光是在
0068
《狹義相對論》
0069
將上式及（0068）代入愛因斯坦公式（0051）內，得
0070
將式（0069）代入愛因斯坦公式（0052）內，有
0071
將式（0070）除以式（0071），得到
0072
上式中t及t'又相抵消了，有
0073
以 上式乘以上式，有
0074
將上式各項重新排列成為
0075
上式（0075）與公式（0067 ）相比較，等號左邊都是Dc右邊也應該相等，即
0076
將上式各式各項重新排列，有的可相加，Gc抵消，得到
0077
以2c 除以上式，有
0078
把式（0078）代入（0075） ，得
0079
上式除以c，有
0080
把式（0080）代入（0059）E=vG 內，得到
0081
然後將式（0081）代入式（0078）中，有
0082
由公式（0080）G=D、式（ 0081 ）E=vD 及式（0082 ）可將E，F，G都換成D。再有一個公式，就可將D解答了。這最後一公式是從條件（2）中得到的。
條件（2）：固定站內的一點 A 變換到開動中街車裡成為 A' 點上，然後又轉回到站內，則必須回到原來的 A 點上，圖 00014 。不然 A 點可隨便改到另外一位置，這是不合理的。
這條件在數學可證明四個系D，E，F，G之間必須有下列關係①：
1=DG-EF
0083
將式 (0080)G=D，式 (0081)E=vD，及式 (0082) D 同時代入式（0083）中，得到
0084
將上式除以 並左右兩邊交換，有
0085
最後將上式兩邊開平方，得
0086
係數D已決定了！其它三個系E，F，G就容易了。
①根據條件（2），數學上可證明在愛因斯坦變換公式中四個係數系的行列式（determinant ）必須等於 1 ，不然 A 點會到另外位置去。愛因斯坦的變換公式是
0051
0052
《狹義相對論》
其行列式是。依照行列式計演演算法，它是等於右對角相乘DG，減去左對角相乘EF。所以有
0083
在線性代數（linerar algebra）中有公式（0083）的更詳細證明法。
將式（0086）代入式（0081）E=vD 中，有
0087
將式（0086）代入式（0082）中，有
0088
最後將式（0086）代入（0080）G=D ，有
0089
四個係數都有了，愛因斯坦的變換公式已推演完成。
將式（0086）及式（0087）代入愛因斯坦公式（0051）內，有
0090
並將式（0088）及式（0089）代入愛因斯坦公式（0052）中，得
0091
其中x及t為車站內或觀察者所在地的位置及時間；
《狹義相對論》
v為街車的速度；
c 為光速。
因為街車的速度v在x方向，其它二方向，（y及z）街車並沒有速度。y與x垂直，z與xy的平面垂直。從式（0090），如以y取代x，y'取代x'及v=0 ，則式（0090）成為y=y'。相同的以z 取代x，z'代x'及v=0 ，則式（0090）成了z=z'。所以有
y=y' 及z=z'
0092
愛因斯坦用了一有趣的字來形容公式（0092）。他的文章寫了在yz方向不應該有什麼“陰謀”( cynical ) 或怪事（ strange ）發生。
公式（0090）及（0091）表明，觀察者在車站內看見街車開動離去。如果觀察者是在街輛，那麼車內的時間是t，位置是x而站上的時間是t'，位置是x'。街車裡的人看到站以速-v退去。公式（53）及（54）可重新排列成為
0093
0094
公式（0093）、（0094）其實與式（0090）是相同的，只是外形不同而已。公式（0090）到（0094）是狹義相對論的主要結果。這一重要理論的關鍵步驟是愛因斯坦的公式 (0052) 。這公式看起來並不是很複雜的，卻引進了不少奇妙的好結果。愛因斯坦根據光速不改變，想到二新的條件也是很有技巧的。
基本信息
- 中文名
- 狹義相對論
- 外文名
- special relativity
- 別名
- 特殊相對論
- 應用學科
- 適用領域
- 在四維時空下的物體、慣性參考系
- 提出時間
- 1905年
- 提出者
- 愛因斯坦、洛倫茲、龐加萊和閔可夫斯基
- 表達式
- S(R⁴,η_αβ)
- 數學工具
- 微分幾何，線性代數
目錄