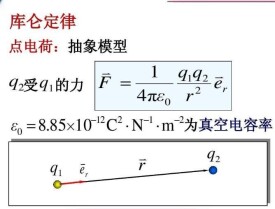
庫侖定律

庫侖定律（Coulomb's law），法國物理學家查爾斯·庫侖於1785年發現，因而命名的一條物理學定律。庫侖定律是電學發展史上的第一個定量規律。因此，電學的研究從定性進入定量階段，是電學史中的一塊重要的里程碑。庫侖定律闡明，在真空中兩個靜止點電荷之間的相互作用力與距離平方成反比，與電量乘積成正比，作用力的方向在它們的連線上，同號電荷相斥，異號電荷相吸。

1.真空中

2.靜止

3.點電荷

（靜止是在觀測者的參考系中靜止，中學計算一般不做要求）

庫侖定律是1784--1785年間庫侖通過扭秤實驗總結出來的。紐秤的結構如下：在細金屬絲下懸掛一根秤桿，它的一端有一小球A，另一端有平衡體P，在A旁還置有另一與它一樣大小的固定小球B。為了研究帶電體之間的作用力，先使A、B各帶一定的電荷，這時秤桿會因A端受力而偏轉。轉動懸絲上端的懸鈕，使小球回到原來位置。這時懸絲的扭力矩等於施於小球A上電力的力矩。如果懸絲的扭力矩與扭轉角度之間的關係已事先校準、標定，則由旋鈕上指針轉過的角度讀數和已知的秤桿長度，可以得知在此距離下A、B之間的作用力。如何比較力的大小【通過懸絲扭轉的角度可以比較力的大小】

靜電學中描述在無限大真空中兩個點電荷q1與q2間作用力的定律。是電磁場理論的基本定律之一。它說明q1對於q2的作用力F與它們之間距離r的平方成反比，與電量q1、q2分別成正比。

式中F 的單位為牛頓(N),q1和q2的單位為庫侖(C),r的單位為米(m)，k為靜電常數，ε0稱為真空介電常數（k=1/4πε0）

力F 的方向沿著兩個點電荷q1和q2的連線。兩電荷異號時，F 為吸力；兩電荷同號時，F 為斥力。

庫侖定律是法國物理學家C.-A.庫侖於 1785年通過扭秤實驗得出的。他使用扭秤測量了作用力，但當時的實驗精度不高。通過間接的方法，可以檢驗平方反比律中指數2的精確程度。J.C.麥克斯韋得出，若令公式中r的方次為2+δ,δ為誤差，則δ的上限為|δ|≤1/21600。1936年，S.J.普林頓和W. E.勞頓通過實驗得出：|δ|＜2×10。1971年,E.R.威廉斯、J.E.費勒和H.A.希爾求得δ的極限值為(2.7±3.1)×10 。此外，E.盧瑟福所做的原子核對α粒子散射的實驗證明：在帶電粒子間近至10cm的核尺度上，庫侖定律仍保持有效。但對於比這小的距離，定律則不成立。

如果真空中有多個點電荷，作用於任一點電荷（如q1）上的總力是其他點電荷分別對於q1的作用力的矢量和。兩個電荷間的作用力不因其他電荷的存在而改變。

如果q1和q2兩個電荷都浸沒在一無限大的均勻、各向同性電介質中，ε為電介質的介電常數。空氣(0℃，1大氣壓時)的ε＝1.00059ε0，ε0為真空介電常數。

COULOMB’S LAW

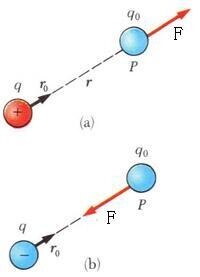
庫侖定律——描述靜止點電荷之間的相互作用力的規律真空中，點電荷 q1 對 q2的作用力為

F=k*(q1*q2)/r^2 (可結合萬有引力公式F=Gm1m2 /r^2來考慮）

其中：

r——兩者之間的距離

r——從 q1到 q2方向的矢徑

k——庫侖常數

上式表示：若q1與q2同號，F12y沿r方向——斥力；

若兩者異號，則F12沿-r方向——吸力.

顯然q2對q1的作用力

F21=-F12（1-2）

在MKSA單位制中

力F的單位：牛頓（N）=千克·米/秒2(kg·m/S2)（量綱：MLT-2）

電量q的單位：庫侖（C）

定義：當流過某曲面的電流1 安培時，每秒鐘所通過的電量定義為 1 庫侖，即

1庫侖（C）=1安培·秒（A·S）（量綱：IT）

比例常數k= 1/4pe0 (1-3)=9.0x10^9牛·米2/庫2

e0=8.854187818(71)×10-12庫2/牛·米2(通常表示為法拉/米 )

是真空介電常數 英文名稱：permittivity of vacuum

說明：又稱絕對介電常數。符號為εo。等於8.854187817×10-12法/米。它是導自真空磁導率和光在真空中速度的一個無誤差常量。

(1)描述點電荷之間的作用力，僅當帶電體的尺度遠小於兩者的平均距離，才可看成點電荷

(2）描述靜止電荷之間的作用力，當電荷存在相對運動時，庫侖力需要修正為Lorentz力。但實踐表明，只要電荷的相對運動速度遠小於光速 c，庫侖定律給出的結果與實際情形很接近。

[例1-1]比較氫原子中質子與電子的庫侖力和萬有引力（均為距離平方反比力）

據經典理論，基態氫原子中電子的“軌道”半徑r ≈ 5.29×10 -11 米

核子的線度≤10-15米，電子的線度≤10-18米，故兩者可看成“點電荷”.

兩者的電量e≈±1.60×10-19庫侖質量m≈1.67×10-27千克me ≈ 9.11×10-31千克

萬有引力常數G ≈6.67×10-11牛 ·米2 /千克2

電子所受庫侖力Fe =-e2r/4pe0r3電子所受引力 Fg= -Gmpmer /r3

兩者之比：Fe/Fg =e2/4pe0Gmpme≈2.27×1039（1-6）

由此可見，電磁力在原子、分子結構中起決定性作用，這種作用力遠大於萬有引力引起的作用力，即可表述為質量對物體間的影響力遠小於電磁力的作用，並且有：電荷之間的作用力隨著電荷量的增大而增大，隨著距離的增大而減小。

庫侖定律可以說是一個實驗定律，也可以說是牛頓引力定律在電學和磁學中的“推論”。假如說它是一個實驗定律，庫侖扭稱實驗起到了重要作用，而電擺實驗則起了決定作用；即便是這樣，庫侖仍然借鑒了引力理論，模擬萬有引力的大小與兩物體的質量成正比的關係，認為兩電荷之間的作用力與兩電荷的電量也成正比關係。假如說它是牛頓萬有引力定律的推論，那麼普利斯特利和卡文迪許等人也做了大量工作。因此，從各個角度考察庫侖定律，重新準確的對它進行熟悉，確實是非常必要的。

人類對電現象的熟悉、研究，經歷了很長的時間。直到16世紀人們才對電的現象有了深入的熟悉。吉爾伯特比較系統地研究了靜電現象，第一個提出了比較系統原始理論，並引人了“電吸引”這個概念。但是吉爾伯特的工作仍停留在定性的階段，進展不大。18世紀中葉，人們藉助於萬有引力定律，對電和磁做了種種猜測。18世紀後期，科學家開始了電荷相互作用的研究。

富蘭克林最早觀察到電荷只分佈在導體表面。普利斯特利重複了富蘭克林的實驗，在《電學的歷史和現狀》一書中他根據牛頓的《自然哲學的數學原理》最先預言電荷之間的作用力只能與距離平方成反比。雖然這個思想很重要，但是普利斯特利的結論在當時並沒有得到科學界的重視。

在庫侖定律提出前有兩個人曾作過定量的實驗研究，並得到明確的結論。可惜，都沒有及時發表而未對科學的發展起到應有的推動作用。一位是英國愛丁堡大學的羅賓遜，認為電力服從平方反比律，並且得到指數n=2.06，從而電學的研究也就開始進行精確研究。不過，他的這項工作直到1801年才發表。另一位是英國的卡文迪許。1772～1773年間，他做了雙層同心球實驗，第一次精確測量出電作用力與距離的關係。發現帶電導體的電荷全部分佈在表面而內部不帶電。卡文迪許進一步分析，得到n=20.02。他的這個同心球實驗結果在當時的條件下是相當精確的。但可惜的是他一直沒有公開發表這一結果。

庫侖是法國工程師和物理學家。1785年，庫侖用扭稱實驗測量兩電荷之間的作用力與兩電荷之間距離的關係。他通過實驗得出：“兩個帶有同種類型電荷的小球之間的排斥力與這兩球中心之間的距離平方成反比。”同年，他在《電力定律》的論文中介紹了他的實驗裝置，測試經過和實驗結果。

庫侖的扭秤巧妙的利用了對稱性原理按實驗的需要對電量進行了改變。庫侖讓這個可移動球和固定的球帶上同量的同種電荷，並改變它們之間的距離。通過實驗數據可知，斥力的大小與距離的平方成反比。但是對於異種電荷之間的引力，用扭稱來測量就碰到了麻煩。經過反覆的思考，庫侖借鑒動力學實驗加以解決。庫侖設想：假如異種電荷之間的引力也是與它們之間的距離平方成反比，那麼只要設計出一種電擺就可進行實驗。

通過電擺實驗，庫侖認為：“異性電流體之間的作用力，與同性電流體的相互作用一樣，都與距離的平方成反比。”庫侖利用與單擺相類似的方法測定了異種電荷之間的引力也與它們的距離的平方成反比，不是通過扭力與靜電力的平衡得到的。可見庫侖在確定電荷之間相互作用力與距離的關係時使用了兩種方法，對於同性電荷，使用的是靜電力學的方法；對於異性電荷使用的是動力學的方法。

庫侖注重修正實驗中的誤差，最後得到：“在進行剛才我所說的必要的修正後，我總是發現磁流體的作用不管是吸引還是排斥都是按距離平方倒數規律變化的。”但是應當指出的是，庫侖只是精確的測定了距離平方的反比關係，並把靜電力和靜磁力從形式歸納於萬有引力的範疇，我們這裡要強調的是庫侖並沒有驗證靜電力與電量之積成正比。“庫侖僅僅認為應該是這樣。也就是說庫侖驗證了電力與距離平方成反比，但僅僅是推測電力與電量的乘積成正比。”

庫侖定律是平方反比定律，自發現以來，科學家不斷檢驗指數2的精度。1971年威廉等人的實驗表明庫侖定律中指數2的偏差不超過10^-16，因此假定為2。事實上，指數為2和光子靜止質量為零是可以互推的。其實假如mz不為零，即使這個值很小，也會動搖物理學大廈的重要基石，因為現有理論都是以mz等於零為前提。到目前為止，理論和實驗表明點電荷作用力的平方反比定律是相當精確的。200多年來，電力平方反比律的精度提高了十幾個數量級，使它成為當今物理學中最精確的實驗定律之一。回顧庫侖定律的建立過程，庫侖並不是第一個做這類實驗的人，而且他的實驗結果也不是最精確的。我們之所以把平方反比定律稱為庫侖定律是因為庫侖結束了電學發展的第一個時期。庫侖的工作使靜電學趨於高度完善。電量的單位也是為了紀念庫侖而以他的名字命名的。

庫侖定律不僅是電磁學的基本定律，也是物理學的基本定律之一。庫侖定律闡明了帶電體相互作用的規律，決定了靜電場的性質，也為整個電磁學奠定了基礎。庫侖從1777年起就致力於把超距作用引入磁學和電學。他認為靜電力和靜磁力都來自遠處的帶電體和荷磁體，並不存在什麼電流體和渦旋流體對帶電物質和磁體的衝擊；這些力都符合牛頓的萬有引力定律所確定的關係。庫侖提供了精密的測量，排除了關於電本性的一切思辯。庫侖的工作對法國物理學家的影響還可以從稍後的拉普拉斯的物理學簡略綱領得到證實。這個物理學簡略綱領最基本的出發點是把一切物理現象都簡化為粒子間吸引力和排斥力的現象，電或磁的運動是荷電粒子或荷磁粒子之間的吸引力和排斥力產生的效應。這種簡化便於把分析數學的方法運用於物理學。

1767年，英格蘭化學家約瑟夫·普利斯特里猜測電荷之間的相互作用力具有類似於萬有引力的的平方反比形式。

1769年，蘇格蘭物理學家約翰·羅比遜首次通過實驗發現兩個帶電球體之間的作用力與它們之間距離的2.06次方成反比。

1770年代早期，著名英國物理學家亨利·卡文迪什通過巧妙的實驗，得出了帶電體之間的作用力依賴於帶電量與距離，並得出靜電力與距離的 成反比，只是卡文迪什沒有公布這個結果。

後來，麥克斯韋利用與卡文迪什類似的方法，得出靜電力與距離的 成反比的結果。

庫侖定律是電學的基本定律，其中平方反比關係是否精確成立尤其重要，而根據現代量子場論，靜電力的平方反比關係是與光子的靜質量是否精確為零相關的，所以，對靜電力的平方反比關係的精確驗證，關係著現代物理學基本理論的基礎。當前對庫侖定律平方反比關係的驗證越來越精確，如1971年進行的一次實驗，給出庫侖定律與平方反比關係的偏差小於。

(1) 庫侖定律只適用於計算兩個點電荷間的相互作用力，非點電荷間的相互作用力，庫侖定律不適用。（不能根據直接認為當r無限小時F就無限大，因為當r無限小時兩電荷已經失去了作為點電荷的前提。）

(2) 應用庫侖定律求點電荷間相互作用力時，不用把表示正,負電荷的"+","-"符號代入公式中計算過程中可用絕對值計算，其結果可根據電荷的正，負確定作用力為引力或斥力以及作用力的方向。

(3)庫侖力一樣遵守牛頓第三定律，不要認為電荷量大的對電荷量小的電荷作用力大。(兩電荷之間是作用力和反作用力) 。

下列關於點電荷的說法，正確的是()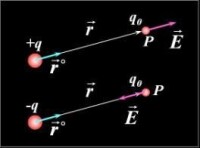A.點電荷一定是電量很小的電荷B.點電荷是一種理想化模型，實際不存在C.只有體積很小的帶電體，才能作為點電荷D.體積很大的帶電體一定不能看成點電荷解析：選B.當帶電體間的距離比它們自身的大小大得多，以至帶電體的形狀、大小及電荷分佈狀況對它們的作用力影響可以忽略時，這樣的帶電體就可以看成點電荷，所以A、C、D錯，B正確.2.關於庫侖定律的公式F=kQ1Q2r2，下列說法中正確的是()A.當真空中的兩個點電荷間的距離r→∞時，它們之間的靜電力F→0B.當真空中的兩個點電荷間的距離r→0時，它們之間的靜電力F→∞C.當兩個點電荷之間的距離r→∞時，庫侖定律的公式就不適用了D.當兩個點電荷之間的距離r→0時，電荷不能看成是點電荷，庫侖定律的公式就不適用答案：AD3.(2011年佛山高二檢測)真空中兩個點電荷Q1、Q2，距離為R，當Q1增大到原來的3倍，Q2增大到原來的3倍，距離R增大到原來的3倍時，電荷間的庫侖力變為原來的()A.1倍 B.3倍C.6倍 D.9倍解析：選A.原來的庫侖力為F=kQ1Q2R2，後來的庫侖力為F′=k3Q1?3Q2?3R?2=kQ1Q2R2=F.所以A對.4.如圖1-2-9所示，兩個質量均為 m 的完全相同的金屬球殼 a和b，其殼層的厚度和質量分佈均勻，將它們固定於絕緣支座上，兩球心間的距離 l 為球半徑的3倍。若使它們帶上等量異種電荷，使其電荷量的絕對值均為Q，那麼關於a、b兩球之間的萬有引力F引和庫侖力F庫的表達式正確的是()圖1-2-9A.F引=Gm2l2，F庫=kQ2l2B.F引≠Gm2l2，F庫≠kQ2l2C.F引≠G m2l2，F庫=kQ2l2D.F引=Gm2l2，F庫≠kQ2l2解析：選D.由於a、b 兩球所帶異種電荷相互吸引，使它們各自的電荷分佈不均勻，即相互靠近的一側電荷分佈較密集，又l=3r，不滿足l?r的要求，故不能將帶電球殼看成點電荷，所以不能應用庫侖定律，故F庫≠kQ2l2.雖然不滿足l?r，但由於其殼層的厚度和質量分佈均勻，兩球殼可看成質量集中於球心的質點，可以應用萬有引力定律，故F引=Gm2l2.5.如圖1-2-10所示，一條長為3L的絕緣絲線穿過兩個質量都是m的小金屬環A和B，將絲線的兩端共同繫於天花板上的O點，使金屬環帶電后，便因排斥而使絲線構成一個等邊三角形，此時兩環恰處於同一水平線上，若不計環與線間的摩擦，求金屬環所帶電量是多少？圖1-2-10解析：小球A受力如圖，受四個力，重力mg、庫侖力F、絲線兩個拉力FT相等。則FTsin60°=mgFTcos60°+FT=kq2L2解得q= 3mgL2k.答案：均為 3mgL2k一、選擇題1.(2011年廣東實驗中學模擬)如圖1-2-11所示，兩個帶電球，大球的電荷量大於小球的電荷量，可以肯定()圖1-2-11A.兩球都帶正電B.兩球都帶負電C.大球受到的靜電力大於小球受到的靜電力D.兩球受到的靜電力大小相等新課標第一網解析：選D.由題圖可知，兩帶電球相互排斥，則說明兩球一定帶有同種電荷，但不能確定是正電荷，還是負電荷，故A、B錯；兩帶電球間的靜電力具有一般力的共性，符合牛頓第三定律，故選項C錯，D對.2.兩個帶正電的小球，放在光滑的水平絕緣板上，它們相距一定距離。若同時釋放兩球，它們的加速度之比將()A.保持不變 B.先增大后減小C.增大 D.減小解析：選A.兩者之間的庫侖力時刻保持大小相等、方向相反，由牛頓第二定律知：a1∶a2=m2∶m1，故A正確.3.(2011年北京四中高二檢測)兩個質量分別為m1、m2的小球，各用長為L的絲線懸掛在同一點，當兩球分別帶同種電荷，且電荷量分別為q1、q2時，兩絲線張開一定的角度θ1、θ2，如圖1-2-12所示，則下列說法正確的是()圖1-2-12A.若m1>m2，則θ1>θ2B.若m1=m2，則θ1=θ2C.若m1θ2D.若q1=q2，則θ1=θ2解析：選BC.這是一道帶電體平衡問題，分析方法仍然與力學中物體的平衡方法一樣.4.要使真空中的兩個點電荷間的庫侖力增大到原來的4倍，下列方法可行的是()A.每個點電荷的電荷量都增大到原來的2倍，電荷間的距離不變B.保持點電荷的電荷量不變，使兩個點電荷的距離增大到原來的2倍C.使一個點電荷的電荷量增加1倍，另一個點電荷的電荷量保持不變，同時使兩點電荷間的距離減小為原來的12D.保持點電荷的電荷量不變，將兩點電荷間的距離減小為原來的12答案：AD5.半徑相同的兩個金屬小球A和B帶有電量相等的電荷，相隔一定距離，兩球之間的相互吸引力的大小是F，今讓第三個半徑相同的不帶電的金屬小球C先後與A、B兩球接觸后移開。這時，A、B兩球之間的相互作用力的大小是()A.18F B.14FC.38F D.34F解析：選A.由庫侖定律，接觸前F=kq2r2，接觸后F′=k12q×14qr2=18kq2r2=18F，故A正確.6.兩個完全相同的小金屬球，它們的帶電荷量之比為5∶1(皆可視為點電荷)，它們在相距一定距離時相互作用力為F1，如果讓它們接觸后再放回各自原來的位置上，此時相互作用力變為F2，則F1∶F2可能為()A.5∶2 B.5∶4C.5∶6 D.5∶9解析：選BD.由庫侖定律，它們接觸前的庫侖力為F1=k5q2r2若帶同種電荷，接觸后的帶電荷量相等，為3q，此時庫侖力為F2=k9q2r2若帶異種電荷，接觸后的帶電荷量相等，為2q，此時庫侖力為F′2=k4q2r2由以上計算可知選項BD正確。新 課 標 第 一 網7.(2011年銅陵一中高二檢測)如圖1-2-13所示，在光滑且絕緣的水平面上有兩個金屬小球A和B，它們用一絕緣輕彈簧相連，帶同種電荷。彈簧伸長x0時小球平衡，如果A、B帶電荷量加倍，當它們重新平衡時，彈簧伸長為x，則x和x0的關係為()圖1-2-13A.x=2x0 B.x=4x0C.x<4x0 D.x>4x0解析：選C.設彈簧原長為l，勁度係數為K，根據庫侖定律和平衡條件列式得kq1q2?l+x0?2=Kx0，k4q1q2?l+x?2=Kx兩式相除：?l+x?24?l+x0?2=x0x，得：x=?l+x0?2?l+x?2?4x0，因l+x>l+x0，由此推斷選項C正確.8.如圖1-2-14所示，三個完全相同的金屬小球a、b、c位於等邊三角形的三個頂點上.a和c帶正電，b帶負電，a所帶電荷量的大小比b的小。已知c受到a和b的靜電力的合力可用圖中四條有向線段中的一條來表示，它應是()圖1-2-14A.F1 B.F2C.F3 D.F4解析：選B.據“同電相斥、異電相引”規律，確定電荷c受到a和b的庫侖力方向，考慮a的帶電荷量小於b的帶電荷量，因此Fb大於Fa，Fb與Fa的合力只能為F2，故選項B正確。二、計算題9.一帶電荷量為+Q、半徑為R的球，電荷在其內部能均勻分佈且保持不變，現在其內部挖去一半徑為R/2的小球后，如圖1-2-15所示，求剩餘部分對放在兩球心連線上一點P處電荷量為+q的電荷的靜電力。已知P距大球球心距離為4R.圖1-2-15解析：未挖去之前，+Q對q的斥力為：F=kQq?4R?2挖去的小球帶電荷量為：Q′=Q4πR33×4π?R2?33=Q8挖去的小球原來對q的斥力為：F1=kQ8q?4R-R2?2=kQq98R2剩餘部分對q的斥力為：F2=F-F1=41kQq784R2，方向向右。答案：41kQq784R2　方向向右10. (2011年廣州高二檢測)光滑絕緣導軌，與水平面成45°角，兩個質量均為m，帶等量同種電荷的小球A、B，帶電量均為q，靜止於導軌的同一水平高度處，如圖1-2-16所示。求：兩球之間的距離。圖1-2-16解析：設兩球之間的距離為x，相互作用的庫侖力為F，則：F=kq2x2由平衡條件得：Fcos45°=mgsin45°由以上兩式解得：x=q kmg.答案：q kmg11.質量均為m的三個帶電小球A、B、C放置在光滑絕緣的水平面上，相鄰球間的距離均為L，A球帶電量qA=+10q;B球帶電量qB=+q.若在C球上加一個水平向右的恆力F，如圖1-2-17所示，要使三球能始終保持L的間距向右運動，問外力F為多大?C球帶電性質是什麼？圖1-2-17解析：由於A、B兩球都帶正電，它們互相排斥，C球必須對A、B都吸引，才能保證系統向右加速運動，故C球帶負電荷。以三球為整體，設系統加速度為a，則F=3ma①隔離A、B，由牛頓第二定律可知：對A：kqAqC4L2-kqAqBL2=ma②對B：kqAqBL2+kqBqCL2=ma③聯立①、②、③得F=70kq2L2.答案：70kq2L2　負電荷。

庫侖定律的常見表述：真空中兩個靜止的點電荷之間的相互作用力，與它們的電荷量的乘積成正比，與它們的距離的二次方成反比，作用力的方向在它們的連線上，同名電荷相斥，異名電荷相吸。

庫侖定律的數學表達式：其中r為兩者之間的距離；為從q1到q2方向的矢徑；k為庫侖常數（靜電力常量）。當各個物理量都採用國際制單位時，用該公式計算時，不要把電荷的正負符號代入公式中，計算過程可用絕對值計算，可根據同名電荷相斥，異名電荷相吸來判斷力的方向。

庫侖定律的微分形式：其中D為電位移矢量，在真空中， E為電場強度，為電荷密度，為真空中的介電常數，實驗測得其大小。該式描述為空間中某一點的電位移矢量的散度等於該處的電荷密度。微分形式的庫侖定理也被稱為電場的高斯定律，是麥克斯韋方程組的一部分。

適用條件

在庫侖定律的常見表述中，通常會有真空和靜止，是因為庫侖定律的實驗基礎——扭秤實驗，為了排除其他因素的影響，是在亞真空中做的。另外，一般講靜電現象時，常由真空中的情況開始，所以庫侖定律中有“真空”的說法。實際上，庫侖定律不僅適用於真空中，還適用於均勻介質中，也適用於靜止的點電荷之間。

庫侖定律還適用於均勻介質中。真空中的庫侖力(d指的是兩電荷之間的距離)，k是一個普適常量，常引入，為真空中的介電常數，實驗測得其大小。根據高斯定理，在均勻無限大介質中（介電常數），兩個點電荷之間的相互作用力是真空中的 倍，即，形式與真空的完全一樣。因此，庫侖定律不僅適用於真空，還適用於介質中。

庫侖定律適用於場源電荷靜止、受力電荷運動的情況，但不適用於運動電荷對靜止電荷的作用力。由於靜止的場源電荷產生的電場的空間分佈情況是不隨時間變化的，所以，運動的電荷所受到的靜止場源電荷施加的電場力是遵循庫侖定律的；靜止的電荷所受到的由運動電荷激發的電場產生的電場力不遵守庫侖定律，因為運動電荷除了激發電場外，還要激發磁場。此時，庫侖力需要修正為電磁力。但實踐表明，只要電荷的相對運動速度遠小於光速c，庫侖定律給出的結果與實際情形很接近。

庫侖定律只適用於點電荷之間。帶電體之間的距離比它們自身的大小大得多，以至形狀、大小及電荷的分佈狀況對相互作用力的影響可以忽略，在研究它們的相互作用時，人們把它們抽象成一種理想的物理模型——點電荷，庫侖定律只適用於點電荷之間的受力。

局限性

庫侖定律沒有解決電荷間相互作用力是如何傳遞的，甚至按照庫侖定律的內容，庫侖力不需要接觸任何媒介，也不需要時間，而是直接從一個帶電體作用到另一個帶電體上的。即電荷之間的相互作用是一種“超距作用”，然而另一批物理學家認為這類力是“近距作用”，電力通過一種充滿在空間的彈性媒介——以太來傳遞。

英國科學家法拉第在研究電場時首先提出場的觀點。他認為電荷會在其周圍空間激發電場，處於電場中的其他電荷將受到力的作用，即電荷與電荷的相互作用時通過存在於它們之間的場來實現的。

現代科學已經證實，相互作用不是“超距”的，但“近距”觀點所假定的以太是不存在的，電荷之間存在相互作用力是通過電場來傳遞的，電荷之間相互作用的傳遞速度是光速。

卡文迪許的同心球電荷分佈實驗，比庫侖的扭秤實驗精確且早幾十年，但是卡文迪許並沒有發表自己的著作。直到1871年麥克斯韋主持劍橋大學的卡文迪許實驗室后，卡文迪許的手稿才轉到了麥克斯韋手中，麥克斯韋親自動手重複了卡文迪許的許多實驗，手稿經麥克斯韋整理后出版，他的工作才為世人所知。

庫侖定律由法國物理學家庫侖於1785年在《電力定律》一論文中提出。庫侖定律是電學發展史上的第一個定量規律，是電磁學和電磁場理論的基本定律之一。

庫侖定律不僅是電磁學的基本定律，也是物理學的基本定律之一。庫侖定律闡明了帶電體相互作用的規律，決定了靜電場的性質，也為整個電磁學奠定了基礎。庫侖的工作對法國物理學家的影響還可以從稍後的拉普拉斯的物理學簡略綱領得到證實。這個物理學簡略綱領最基本的出發點是把一切物理現象都簡化為粒子間吸引力和排斥力的現象，電或磁的運動是荷電粒子或荷磁粒子之間的吸引力和排斥力產生的效應。這種簡化便於把分析數學的方法運用於物理學。

電量的單位是為了紀念庫侖而以他的名字命名的。 （符號是Q，單位庫侖，符號C）