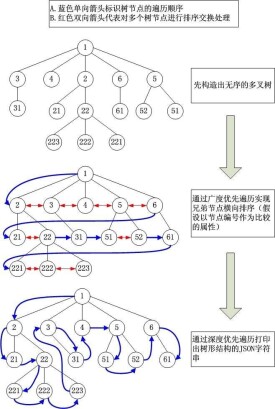
n叉樹
n叉樹
樹家族是為了實現方便快捷的查找而存在的。樹的高度是命中查找的一個不可抗拒的時間下限。在一定的數據條件下,樹的高度和寬度是互相制約的。(就像一定面積下,矩形的長和寬是互相制約的)而樹家族中最簡單的二叉樹,儘管易於實現,卻不能有實際的價值。其最最令人髮指的是二叉樹的高度太高。n叉樹的提出和實現解決了二叉樹的不足,典型的n叉樹有:2-3-4樹/紅黑樹和B樹。
二叉樹中每個結點有一個數據項,最多有兩個子節點,如果允許樹的每個節點可以有兩個以上的子節點,那麼這個樹就稱為n階的多叉樹,或者稱為n叉樹。
• 每個節點有m個子節點和m-1個鍵值。
• 每個節點中的鍵值按升序排列。
• 前i個子節點中的鍵值都小於第i個鍵值。
• 后m-1個子節點中的鍵值都大於第i個鍵值。
典型的n叉樹有2-3-4-Tree和B-Tree兩種。
B樹(B-tree)是有Bayer和McCreight在1972年提出的數據結構。B樹索引是資料庫中存取和查找文件(稱為記錄或鍵值)的一種方法,應用於磁碟讀取方面。
B樹(B-tree)是一種樹狀數據結構,它能夠存儲數據、對其進行排序並允許以O(log n)的時間複雜度運行進行 查找、順序讀取、插入和 刪除的數據結構。B樹,概括來說是一個節點可以擁有多於2個子節點的二叉查找樹。與自平衡二叉查找樹不同,B樹為系統最優化大塊數據的讀和寫操作。B-tree演演算法減少定位記錄時所經歷的中間過程,從而加快存取速度。普遍運用在資料庫和文件系統。
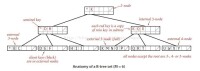
B樹
根據Knuth's的定義,n階B樹(a B-tree of order n)是具有以下性質:
• 每個點最多有n個孩子
• 每個非葉子節點(根節點除外)最多有n/2(向上取整)個孩子
• k個孩子的非葉子節點含有k-1個鍵值
• 所有的葉子節點都在同一層,並且內部節點不攜帶任何信息。(B樹的階指最大子節點數。優勢,n階的B樹節點定義為有k個鍵值和k+1個指針,其中n<=k<=2n,用於指定最少的子節點數)
注意:根結點為葉子節點,整棵樹只有一個根節點。
2-3-4樹在計算機科學中是階為4的B樹。大體上同B樹一樣,2-3-4樹是可以用做字典的一種自平衡數據結構。它可以在O(logn)時間內查找、插入和刪除,這裡的n是樹中元素的數目。2-3-4樹在多數編程語言中實現起來相對困難,因為在樹上的操作涉及大量的特殊情況。紅黑樹實現起來更簡單一些,所以可以用它來替代。
2-3-4樹把數據存儲在叫做元素的單獨單元中。2-3-4樹,就是有2個子女,3個子女,或4個子女的節點,這些含有2、3、或4個子女的節點就構成了我們的2-3-4樹。所以,它們組合成節點,每個節點都是下列之一:
• 2-節點,就是說,它包含1個元素和2個子節點
• 3-節點,就是說,它包含2個元素和3個子節點
• 4-節點,就是說,它包含3個元素和4個子節點
每個子節點都是(可能為空)一個子2-3-4樹。根節點是其中沒有父節點的那個節點;它在遍歷樹的時候充當起點,因為從它可以到達所有的其他節點。葉子節點是有至少一個空子節點的節點。同B樹一樣,2-3-4樹是有序的:每個元素必須大於或等於它左邊的和它的左子樹中的任何其他元素。每個子節點因此成為了由它的左和右元素界定的一個區間。如下圖所示(你可以看到,圖中這棵2-3-4樹是由2-結點,3-結點,4-結點元素組成的):
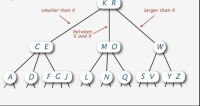
2-3-4樹
儘管2-3-4樹的流行和其簡單實現(紅黑樹)已經逐漸被大家接納,但是對於大量數據來說,用紅黑樹實現查找是不現實的。MySQL和Berkeley DB都是基於B樹原理而建立資料庫的。B樹是一種可實現的平衡多路查找樹。此次對B樹的實現進行舉例。
偽代碼如下: