第二型曲線積分

第二型曲線積分的物理背景是變力沿曲線做功。

空間中有一變力作用在某質點上，使其從某一曲線L的端點A，沿著L移動到另一端點B，求該力做功多少？

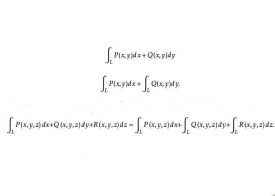
顯然在L上取一有向弧微元則可得做功微元，那麼力 F移動質點從A到B所做的功為，若用坐標表示，則成為

這種類型的積分稱為 第二型的曲線積分。

定義1設函數定義在平面有向可求長度曲線L上，對L的任意分割T，它把L分成n個小弧段：在每個小曲線段上任取一點，若極限存在，且與分割T和點 的取法無關，其中||T||是各小弧段長度的最大值，則稱此極限為函數，沿有向曲線L上的第二型曲線積分，記為

或

定義2 設L為空間內一條光滑有向曲線，函數在L上有定義，則可以定義沿空間有向曲線L上的第二型曲線積分，並記為

(1)如果把L分成和，且都存在，則

(2)設L是有向曲線弧，-L是與L方向相反的有向曲線弧，則

(3)若 存在，則 也存在，且

轉化為定積分，要注意的是：二型線積分的起點，對應定積分的下限，終點對應定積分的上限，即若曲線

則