通徑
圓錐曲線的參數
定義
聯結橢圓上任意兩點的線段叫作這個橢圓的弦,通過焦點的弦叫作這個橢圓的焦點弦(所以橢圓的長軸也是焦點弦),和長軸垂直的焦點弦叫作這個橢圓的通徑(正焦弦)。聯結橢圓上任意一點與一個焦點的線段(或這線段的長)叫作橢圓在這點的焦半徑,橢圓上任意一點有兩條焦半徑。
設橢圓的方程為
如圖1,令解得則其通徑的長為,或(其中e為橢圓的離心率,p為橢圓的焦准距)。
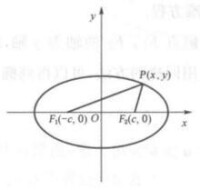
圖1
參數方程與離心率
橢圓的參數方程:的參數方程為(為參數)
說明:
(1)橢圓的長軸與短軸的交點叫做橢圓的中心。
(2)若a為長半軸長,b為短半軸長,為半焦距,為離心率。
(3)離心率表示橢圓的扁鼓程度,離心率越大,橢圓越扁平;離心率為0時,即,此時橢圓為一個圓。
橢圓的焦准距:焦點與相應準線的距離稱為橢圓的焦准距,也叫焦參數。設p為焦距,則:
經過拋物線的焦點,作一條垂直於它的對稱軸的直線,這直線與拋物線有兩個交點,這兩個交點之間的線段叫做拋物線的通徑。
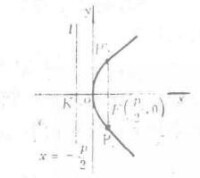
圖2
如圖2所示,拋物線的通徑顯然等於。令解得故通徑長為jie'de解得故通徑長為。
同樣,其它形式的拋物線的通徑長均為。
過雙曲線的焦點與雙曲線的實軸垂直的直線被雙曲線截得的線段的長,稱為雙曲線的通徑。設雙曲線的方程為如圖3,令,解得故其通徑的長為,或(其中a為實軸長,b為虛軸長,e為雙曲線的離心率,p為雙曲線的焦准距)。
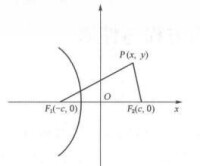
圖3
