等腰梯形
兩腰相等的梯形
等腰梯形(英文:isoscelestrapezium)按照數學領域可定義為:一組對邊平行(不相等),另一組對邊不平行但相等的四邊形。等腰梯形是一個平面圖形,是一種特殊的梯形。
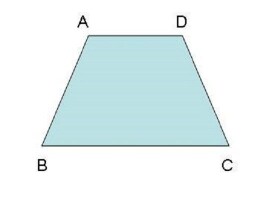
一組對邊平行(不相等),另一組對邊不平行但相等的四邊形叫做等腰梯形。顧名思義,它是梯形的一種特殊情況,即兩腰相等的梯形。在等腰梯形中,如圖1,平行的兩邊叫做梯形的底邊,較長的一條底邊叫下底,即BC,較短的一條底邊叫上底,即AD。另外兩邊叫腰,即AB和CD。夾在兩底之間的垂線段叫梯形的高。
1、等腰梯形同一底上的兩個內角相等。
2、兩腰相等,兩底平行,對角線相等。
3、由托勒密定理可得等腰梯形ABCD,如下圖,有。
5、兩條對角線相等,即
6、等腰梯形的面積公式:。
7、特殊面積計算:當對角線垂直時:,。
8、等腰梯形對角線的平方等於腰的平方與上、下底積的乘積和
9、等腰梯形是軸對稱圖形,只有一條對稱軸,過上下兩底中點的直線即為對稱軸。
1、一組對邊相等且不平行,另一組對邊平行的四邊形是等腰梯形。
2、同一底上的兩個角相等的梯形是等腰梯形。
3、對角線相等的梯形是等腰梯形。
4、兩腰相等的梯形是等腰梯形
以下判定不作為定理使用:
5、對角線相等且能形成兩個等腰三角形的四邊形是等腰梯形。
6、對角互補的梯形是等腰梯形。
;
用a、b、h分別表示梯形的上底、下底、高,“S”表示梯形的面積,則。
特殊情況:
1.若對角線互相垂直,則面積為兩對角線的乘積。
2.在已知中位線情況下,中位線×高。
面積推導:
設有兩個完全一樣的等腰梯形,將這兩個梯形拼成一個平行四邊形,則
平行四邊形底=等腰梯形上底和下底之和,平行四邊形高=等腰梯形的高,設上底為a,下底為b,高為h,則平行四邊形面積,所以等腰梯形面積。
等腰梯形的周長=上底+下底+2×腰,設等腰直角形上底為a,下底為b,腰為c,高為h,周長為c
(1)已知上底、下底、腰,計算周長
。
(2)已知上底、下底、高
推導如下:
根據勾股定理,可求得腰長為:
故,等腰梯形周長為:
一些平面幾何問題中,常用於等腰梯形的輔助線如圖4所示。
● ● 平移一腰到梯形內;
● ● 平移一腰到梯形外;
● ● 作等腰梯形的對角線;
● ● 過中點平移兩腰;
● ● 平移一條對角線;
● ● 過一腰的中點作另一腰的平行線;
● ● 過上底兩點向下底兩點做垂線;
● ● 頂點連一腰的中點並延長;
● ● 延長兩腰交於一點。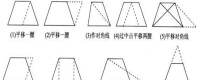

等腰梯形