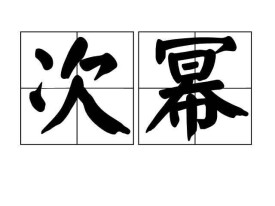
次冪

新華字典解釋

冪（mì）形聲。從巾，冥聲。

1）本義：蓋東西用的巾。【英語 cloth cover】

大巾謂之冪。——《小爾雅·廣詁》

冪人，掌共巾冪。——《周禮·天官·冪人》。注:“共巾，可以覆物。”

冪用錫若絺。——《儀禮·大射禮》。注:“冪，覆尊巾也。”

冪用疏布。——《儀禮·既夕禮》

簠有蓋冪。——《儀禮·公食大夫禮》

又如：冪首（古代婦女障面的一種頭巾）；冪人(《周禮》官名。掌共巾冪)；冪籬（古代少數民族的一種頭巾）。

2）覆蓋；罩。動詞。

祭祀，以疏布巾冪八尊，以畫布巾冪六彝。——《周禮·天官·冪人》

青煙冪處，碧海飛金鏡。——晁補之《洞仙歌》

3）數學名詞。又稱乘方。表示一個數自乘若干次的形式，如a自乘n次的冪為a^n ，或稱a^n為a的n次冪。【英語 power】a稱為冪的底數，n稱為冪的指數。在擴充的意義下，指數n也可以是分數、負數，也可以是任意實數或複數。

4）雲南少數民族計算布帛的單位。

英漢字典解釋

⒈to cover with cloth

⒉a cloth cover; a veil

⒊[Mathematics] power

部首筆畫

部首

冖

部外筆畫：9

總筆畫：12

五筆86：PJDH

五筆98：PJDH

倉頡：BAKB

筆順編號：452511134252

四角號碼：37227

Unicode：CJK 統一漢字 U+5E42

介紹

冪（power）指乘方運算的結果，n^m指將n自乘m次(根據六下課本該式意義為m個n相乘）把n^m看作乘方的結果，叫做n的m次冪。

數學中的“冪”，是“冪”這個字面意思的引申，“冪”原指蓋東西的布巾，數學中“冪”是乘方的結果，而乘方的表示是通過在一個數字上加上標的形式來實現的，故這就像在一個數上“蓋上了一頭巾”，在現實中蓋頭巾又有升級的意思，所以把乘方叫做冪正好契合了數學中指數級數快速增長含義，形式上也很契合，所以叫做冪。

圓冪定理中的“冪”，則是跟圓冪的定義有關，圓冪是指平面上任意一點到圓心的距離與半徑的平方差，其結果，當點在圓外時，就是切線的長度的平方，而切線的平方本身就是個“冪”，所以為了簡潔，將與圓有關的切線定理、割線定理、相交弦定理統稱為“圓冪定理”。

其中，n稱為底數，m稱為指數（寫成上標）。當不能用上標時，例如在編程語言或電子郵件中，通常寫成n^m或n**m，也可以用低德納箭號表示法，寫成n↑m，讀作“n的m次方”或者n的m次冪。

當指數為1時，通常不寫出來，因為那和底的數值一樣；指數為2、3時，可以讀作“n的平方”、“n的立方”。　n^m的意義亦可視為1×n×n×n...︰起始值1（乘法的單位元）乘底指數這麼多次。這樣定義了后，很易想到如何一般化指數0和負數的情況︰任何非零數數的零次方都是1，即n^0=1（n≠0）；冪的指數是負數時，即n^m=1/n^（-m），（m<0）

分數為指數的冪定義為x^m/n = n√x^m

冪不符合結合律和交換律。

因為十的次方很易計算，只需在後加零即可，所以科學記數法（科學計數法：將一個數字錶示成（a×10的n次冪的形式），其中1≤|a|<10，n表示整數，這種記數方法叫科學記數法。）藉助此簡化記錄數的方式；二的次方在計算機科學中很有用。

同底數冪：a^nxa^m=a^(n+m)；a^n/a^m=a^(n-m)

1.同底數冪的意義：

同底數冪是指底數相同的冪

積的乘方：(axb)^n=a^n×b^n

一點P對半徑R的圓O的冪定義如下：OP^2-R^2，所以圓內的點的冪為負數，圓外的點的冪為正數，圓上的點的冪為零。

圓冪定理是相交弦定理、切割線定理及割線定理(切割線定理推論)以及他們推論的統稱。相交弦定理：圓內的兩條相交弦，被交點分成的兩條線段長的積相等。

切割線定理：從圓外一點引圓的切線和割線，切線長是這點到割線與圓交點的兩條線段長的比例中項。

割線定理：從圓外一點P引兩條割線與圓分別交於A.B.C.D 則有 PA·PB=PC·PD。

統一歸納：過任意不在圓上的一點P引兩條直線L1、L2，L1與圓交於A、B（可重合，即切線），L2與圓交於C、D（可重合），則有PA·PB=PC·PD。

進一步升華（推論）：過任意在圓O外的一點P引一條直線L1與一條過圓心的直線L2，L1與圓交於A、B（可重合，即切線），L2與圓交於C、D。則PA·PB=PC·PD。若圓半徑為r，則PC·PD=(PO-r)·(PO+r)=PO^2-r^2=|PO^2-r^2| （一定要加絕對值，原因見下）為定值。這個值稱為點P到圓O的冪。（事實上所有的過P點與圓相交的直線都滿足這個值）

若點P在圓內，類似可得定值為r^2-PO^2=|PO^2-r^2|

故平面上任意一點對於圓的冪為這個點到圓心的距離與圓的半徑的平方差的絕對值。（這就是“圓冪”的由來）

圓的方程通常表示為x^2+y^2=r^2

1相關介紹：冪指乘方運算的結果。n^m指將n自乘m次(根據六下課本該式意義為m個n相乘）。把n^m看作乘方的結果，叫做n的m次冪。

其中，n稱為底數，m稱為指數（寫成上標）。當不能用上標時，例如在編程語言或電子郵件中，通常寫成n^m或n**m，亦可以用低德納箭號表示法，寫成n↑m，讀作“n的m次方”或者n的m次冪。

當指數為1時，通常不用寫出來，因為那和底的數值是一樣的；指數為2、3時，可以讀作“n的平方”、“n的立方”。　n^m的意義亦可視為1×n×n×n...︰起始值1（乘法的單位元）乘底指數這麼多次。這樣定義了后，很易想到如何一般化指數0和負數的情況︰除了0之外所有數的零次方都是1，即n^0=1；冪的指數是負數時，等於1/n^m。

分數為指數的冪定義為x^m/n = n√x^m

冪不符合結合律和交換律。

因為十的次方很易計算，只需在後加零即可，所以科學記數法是（科學計數法：將一個數字錶示成（a×10的n次冪的形式），其中1≤|a|<10，n表示整數，這種記數方法叫作科學記數法。）藉助此簡化記錄數的方式；二的次方在計算機科學中很有用。

圓冪定理：同底數冪：a^nxa^m=a^(n+m)；a^n/a^m=a^(n-m)

法則

1.同底數冪的意義

同底數冪是指底數相同的冪

積的乘方：(axb)^n=a^n×b^n；

圓冪的定義:

一點P對半徑R的圓O的冪定義如下：OP^2-R^2

所以圓內的點的冪為負數，圓外的點的冪為正數，圓上的點的冪為零。

圓冪定理是相交弦定理、切割線定理及割線定理(切割線定理推論)以及他們推論的統稱。

相交弦定理：圓內的兩條相交弦，被交點分成的兩條線段長的積相等。

切割線定理：從圓外一點引圓的切線和割線，切線長是這點到割線與圓交點的兩條線段長的比例中項。

割線定理：從圓外一點P引兩條割線與圓分別交於A.B.C.D 則有 PA·PB=PC·PD。

統一歸納：過任意不在圓上的一點P引兩條直線L1、L2，L1與圓交於A、B（可重合，即切線），L2與圓交於C、D（可重合），則有PA·PB=PC·PD。

進一步升華（推論）：

過任意在圓O外的一點P引一條直線L1與一條過圓心的直線L2，L1與圓交於A、B（可重合，即切線），L2與圓交於C、D。則PA·PB=PC·PD。若圓半徑為r，則PC·PD=(PO-r)·(PO+r)=PO^2-r^2=|PO^2-r^2| （一定要加絕對值，原因見下）為定值。這個值稱為點P到圓O的冪。（事實上所有的過P點與圓相交的直線都滿足這個值）

若點P在圓內，類似可得定值為r^2-PO^2=|PO^2-r^2|

故平面上任意一點對於圓的冪為這個點到圓心的距離與圓的半徑的平方差的絕對值。（這就是“圓冪”的由來）

圓的方程通常表示為x^2+y^2=r^2