不等邊三角形

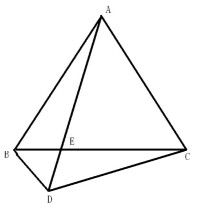
三條邊都不相等的三角形叫不等邊三角形。

不等邊三角形的內心I、垂心H、界心K及其旁心三角形的外心M是平行四邊形的四個頂點。

為了證明上述性質，先說明幾個引理。

引理1：中為三邊上的高，垂心為H，則該三角形三邊之中點，三個垂足三線段之中點九點共圓，且線段之中點連線線段的中點是九點圓圓心。

引理2：設外心為O、垂心為H、則線段OH之中點是九點圓圓心。

引理3：的內心是其旁心三角形的垂心。

引理4：設不等邊的外心為O、垂心為H、內心為I、界心為K。則OI平行且等於二分之一的KH。

性質證明：

設不等邊的旁心三角形為(如圖1)，分別為外心、內心、垂心、界心。由引理4，OI平行且等於二分之一的KH；由引理3及其證明過程知，內心I為旁心的垂心，且直線，直線，直線，又由引理1知，九點圓圓心為外心O；設外心為M，由引理2，有外心M與垂心I的連線線段中點應為九點圓圓心O，故共線且。由OI平行且等於二分之一的 KH，有MI平行且等於KH，即四邊形MIHK為平行四邊形。故△ ABC的內心I、垂心H、界心K及旁心三角形的外心M構成平行四邊形的四個頂點。命題得證。