流變性

1．阿侖尼烏斯方程

微分式：

指數式：

積分式：

式中，A稱為指前因子或表觀頻率因子，其單位與k相同；Ea稱為阿累尼烏斯活化能(簡稱活化能)，其單位為kJmol-1。上述三式是定量表示k與T之間的關係。常用於計算不同溫度T所對應之反應的速率常數k(T)以及反應的活化能Ea。阿倫尼烏斯方程只能用於基元反應或有明確級數而且k隨溫度升高而增大的非基元反應。若溫度變化過大，則阿倫尼烏斯方程會產生誤差，這時，下列方程更好地符合實驗數據

k=ATBexp(-E/RT)

從分子運動觀點看，當大分子熱運動隨溫度升高而增加時，熔體中分子間的空穴(即自由體積)也隨之增加和膨脹，使流動阻力減小。要是以粘度7表示阻力的大小，則在溫度變化不大的範圍內熔體粘度與溫度之間的關係可用Arrhe-nius方程表示：

η=Aexp(Ea/RT)

式中A是常數，R是氣體常數，T是絕對溫度，Ea為流動活化能，它既是大分子向空穴躍遷時克服周圍分子的作用所需要的能量，也是熔體粘度對溫度敏感程度的量度，即Ea越大，粘度對溫度的變化越敏感。(即流動活化能增大，流體的流動性變差。反之，流動活化能減小，流體的流動性變好)

將Arrhe-nius方程兩邊取對數，得到：

lgη=lgA+Ea/2.303RT

然後根據數據作lgη—1/T圖，從所得直線的斜率可計算出Ea.

流體在受到外部剪切力作用時發生變形(流動)．接內部相應要產生對變形的抵抗，並以內摩擦的形式表現出來。所有流體在有相對運動時都要產生內摩擦力，這是流體的一種固有物理屬性，稱為流體的粘滯性或粘性。牛頓內摩擦定律或牛頓剪切定律對流體的粘性作了理論描述，即流體層之間單位面積的內摩擦力或剪切應力與速度梯度或剪切速率成正比。用公式表示如下：

τ=μ(dvx/dy)=μγ

上式又稱為牛頓剪切應力公式，式中的比例係數μ就是代表流體粘滯性的物理量，反映了流體內摩擦力的大小，稱為流體的動力粘性係數或粘度。流體的粘度與溫度有密切的關係。液體的粘度隨著溫度升高而下降，而氣體的粘度則隨著溫度的升高而升高。在物理意義上，牛頓剪切應力公式表明有一大類流體，它們的剪切應力與速度梯度呈線性關係。這類流體被稱為牛頓流體。另一方面，如果上式的函數關係是非線性的，所描述的流體就被稱為非牛頓流體。

為了方便描述非牛頓型流體，人們提出了廣義的牛頓剪切應力公式：

τ=η(dvx/dy)=ηγ

係數η同樣反映流體的內摩擦特性，常常稱為廣義的牛頓粘度。對牛頓型流體，η當然就是粘度，屬於流體的特性參數。對非牛頓型流體，問題就變得複雜起來，η不再是常數，它不僅與流體的物理性質有關，而且還與受到的剪切應力和剪切速率有關，即流體的流動情況要改變其內摩擦特性。人們提出了幾個描述非牛頓型流體內摩擦特性的流變方程模型。如Ostwald—dewaele的冪律模型，Ellis模型，Carreau模型，Bingham模型等。其中冪律模型最為常用。冪律模型認為，非牛頓型流體的粘度函數是速度梯度或剪切速率絕對值的一個指數函數，其表達式為:

1.τ=K(dvx/dy)n=Kγ^n

或者

2.η=K(dvx/dy)n=Kγ^(n-1)

式中，K為稠度係數，N·S”/m2；為流體特性指數，無因次，表示與牛頓流體偏離的程度。

由2式可見：

①當n=1時，η=K，即K具有粘度的因次．此時流體為牛頓流體，可用以檢查所得結果正

確與否；

②當η<1時，為假塑性或剪切變稀流體；

③當η>l時，為膨脹塑性或剪切增稠流體；

④1式從使用觀點看，僅有兩參數，因此被廣泛應用，工業上80%以上的非牛頓流體均可用此模型計算。

在一定的溫度下，流體在外力的作用下呈層流時，流速不同的層間產生內摩擦力，將阻礙液層的相對運動，層流間剪切應力(τ)與流速梯度(dv/dy)之間呈一複雜的關係，並隨著時間、溫度、流體性質和流速不同而產生很大的差別。反映這一關係的基本數學公式就是牛頓流動定律：

τ=η(dvx/dy)

其中，τ——剪切應力（平行流動方向的單位面積上的內摩擦力）

dv/dy——剪切速率（垂直流動方向的流速梯度）

η——粘度（動力粘滯係數）

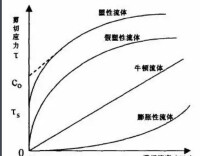
流體的剪切應力與剪切速率之間的變異關係用圖形表示則稱為流變曲線。

塑性流體是非牛頓流體中的一種，其特點是剪切應力小於某一數值τ。時，就不能流動，大於τ。后才開始流動；假塑性流體也是非牛頓流體一種，其流動特點是一旦施加外力就能流動，其粘度隨著剪切速率的增加而減小，流動曲線為通過坐標原點凸向剪切應力軸的曲線；牛頓流體在流變曲線上，剪切應力與剪切速率間關係為一通過原點的直線關係；膨脹性流體也是非牛頓流體中的另一種類型，其特點是一加外力就能流動，粘度隨著剪切速率增加而增大，流動曲線為通過坐標原點凹向剪切應力軸的曲線。

屈服——塑性是指流體在較小外力作用下，不發生流動，只產生有限的彈性變形，只有當外力大於某值時，流體才發生流動，使流體發生流動時對應的剪切應力稱之為屈服應力。

觸變性表述這樣的現象：物體經長時間高剪切從高粘凝膠態變為粘度低得多的溶膠。觸變性的一個重要標誌是物體保持靜止後有重新稠化的可逆過程。這類流體的粘度不僅隨剪切速率變化，而且在恆定的剪切速率下，它的粘度也隨著時間的推移而下降，並達到一個常數值。當剪切作用停止后，粘度又隨時間的推移而增高，大多數觸變性流體，經過幾小時或更長的時間，可以恢復到初始的粘度值。它的曲線形態表現為，在流動曲線圖中“上行曲線”不再與“下行曲線”重疊，而是兩條曲線之間形成了一個封閉的“梭型”觸變環。這個“梭型”觸變環的面積大小決定著觸變特性的量度，它表示破壞觸變結構所需要的能量。

流體可分為牛頓流體和非牛頓流體。其中非牛頓流體還可分為時間獨立性流體(a．假塑體，b．膨脹體，C．塑性假塑體，d．塑性膨脹體)、時間相關性流體(觸變物質和振凝性流體)以及粘彈性流體(線性粘彈體和非線性粘彈體)

非牛頓流體包括剪切變稠型（脹流型）、剪切變稀型、假塑型、塑性型、觸變型以及震凝型流體等。剪切變稠型：粘度隨流速梯度增大而增大，這是因為當顆粒濃度很高並接近最緊密排列時，兩層間的相對運動將使顆粒偏離最緊密排列，體積有所增加，需消耗額外能量。或者因為當流速增加而使顆粒動能增高時，可能越過能壘Eb到達第一極小Em1而發生絮凝，使粘度增大。

剪切變稀型：粘度隨流速梯度增大而減小。這是因為在h較大時，位能曲線上有一個第二極小Em2，它將導致顆粒間形成較弱的絮凝，而流速增大時將破壞這種絮凝使粘度減小。也可能因為顆粒為棒狀或片狀，靜止時顆粒運動受阻，當受到剪切時，顆粒因形成隊列而粘度減小。

粘度隨流速梯度增大而減小，它的剪切變稀的性質更為突出。

該類流體由於絮凝很強而形成網路結構，其特點是存在屈服應力τB，τ<τB時流體僅發生彈性形變。當τ>τB時，網路破壞並開始流動，剪切應力隨流速梯度而變化。

在剪切作用下可由粘稠狀態變為流動性較大的狀態，而剪切作用取消后，要滯后一段時間才恢復到原來狀態。這是由於絮凝網路經剪切破壞后，重新形成網路需要一定時間。

該流體能在剪切作用下變稠。剪切取消后，也要滯后一段時間才恢復變稀。