膠體粘度
膠體粘度
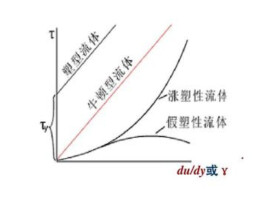
膠體粘度,根據不同的流動-形變性能,流體的流型可分為牛頓型和非牛頓型(塑性、假塑性、脹流型)。
最早研究稀濃度膠體的是A.愛因斯坦,他在1911年得出下列公式:
η=η0(1+2.5φ) (φ<0.1)
式中η0和η分別為溶劑和稀濃度膠體的粘度;φ為膠體質點的體積分數。得出上式時,他除了運用流體力學知識外,還藉助下列假設:①膠體質點是比溶劑分子大得多的球;②球是剛體,且能被不可壓縮的溶劑完全潤濕;③濃度極稀,流體經過質點時,各流層所遭受的擾亂不至於相互干擾;④體系中無紊流。該式曾用已知尺寸的細玻璃球和某種酵母驗證,在濃度很稀時,理論與實驗數據相符。該式說明相對粘度與質點性質和大小無關,粘度的增加只是因為流體受到更大的切應力。實際上,質點的大小、多分散性和溶劑化作用等都影響粘度。
對於稍濃一點的膠體,用下列公式表示:
η=η0(1+2.5φ+K1φ +…)
式中K1是參數,根據不同的模型,可算得不同的數值。
若膠體是非球形的不規則質點,流體流經其質點邊緣時,質點可以轉動,從而消耗了額外的能量。此外,質點之間的相互干擾也是必須考慮的重要因素。濃度稀時,R.西馬就旋轉的橢圓體推導出下式:式中a、b分別是橢圓體的長軸和短軸;λ為常數,扁長旋轉橢圓體的λ是1.5,圓體形棒的λ是1.8。該式曾用不同粒徑的煙草斑紋病毒驗證,在a/b=20.3~64.3,φ<0.003範圍內,理論與實驗結果符合得很好。
當質點相互間有作用,並能形成網狀結構時,還會有一部分溶劑包含在其中,從而使膠體粘度大大增加,因為不但能流動的溶劑減少,而且拆散網狀結構或使其變形,都需要能量。此種因結構而生出的粘度叫結構粘度。它與所施的剪切力有很大關係。剪切力小時,結構粘度大;剪切力增加后,網狀結構被拆散,質點還會隨之定向,故粘度下降。一般濃的膠體和高聚物溶液,皆有此現象。
對親液膠體的粘度,特別是無規線團高聚物溶液的粘度,H.F.馬克和R.豪溫克用兩參數的經驗公式,將其特性粘度[η]同分子量Μ關聯起來。
【η】=KMα
式中K和α為參數。大量實驗數據表明,α在0.5~1.0之間變化。使用良溶劑時,線型高聚物的α為0.6~0.8。加入不良溶劑后,α值逐漸減小;在接近沉澱點時,α值接近1/2。對於內旋轉阻礙較大的剛性高聚物鏈,α值接近1.0。
為了求得[η],必須進行一系列粘度測定,其中有相對粘度(ηr)、增比粘度、比濃粘度和比濃對數粘度。c為濃度,且:通常,取4~5個不同濃度的溶液,測定其η和η0,利用稀釋外推方法,即可求得【η】(見圖)。即以ηSP/c對c和以ln(ηr/c)對c作圖,分別得到兩條直線,外推后,與縱坐標交於同一點,其截距為【η】·c,從而得到【η】。
影響高聚物粘度的因素甚多,如溶液濃度、溶劑種類、溫度、剪切速率、高聚物鏈的聚集狀態及其相互作用等。