剛體
理想化的力學模型
在運動中和受力作用后,形狀和大小不變,而且內部各點的相對位置不變的物體。絕對剛體實際上是不存在的,只是一種理想模型,因為任何物體在受力作用后,都或多或少地變形,如果變形的程度相對於物體本身幾何尺寸來說極為微小,在研究物體運動時變形就可以忽略不計。把許多固體視為剛體,所得到的結果在工程上一般已有足夠的準確度。但要研究應力和應變,則須考慮變形。由於變形一般總是微小的,所以可先將物體當作剛體,用理論力學的方法求得加給它的各未知力,然後再用變形體力學,包括材料力學、彈性力學、塑性力學等的理論和方法進行研究。
簡介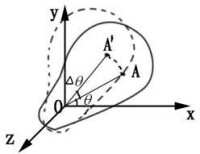 剛體在空間的位置,必須根據剛體中任一點的空間位置和剛體繞該點轉動時的位置(見剛體一般運動)來確定,所以剛體在空間有六個自由度。在很多情況下,固體在受力和運動過程中變形很小,基本上保持原來的大小和形狀不變。對此,人們提出了剛體這一理想模型。就是在任何情況下形狀和大小都不發生變化的物體,其特點是:在運動過程中,剛體的所有質元之間的距離始終保持不變。因此,構成剛體的質元只能以非常受限制的方式彼此相對運動。而且,作用在剛體各個部分之間的內力,在剛體的整體運動中不起作用。剛體是力學中的一個科學抽象概念,即理想模型。事實上任何物體受到外力,不可能不改變形狀。實際物體都不是真正的剛體。若物體本身的變化不影響整個運動過程,為使被研究的問題簡化,可將該物體當作剛體來處理而忽略物體的體積和形狀,這樣所得結果仍與實際情況相當符合。例如,物理天平的橫樑處於平衡狀態,橫樑在力的作用下產生的形變很小,各力矩的大小都幾乎不變。對於形變,實際是存在的,但可不予考慮。為此在研究天平橫樑平衡的問題時,可將橫樑當作剛體。在外力作用下,物體的形狀和大小(尺寸)保持不變,而且內部各部分相對位置保持恆定(沒有形變),這種理想物理模型稱之為剛體。剛體是個理想模型。如果物體的剛性足夠大,以致其中彈性波的傳播速度比該物體的運動速度大很多,從而可以認為彈性擾動的傳播是瞬時的,就可以把該物體當作剛體處理。在剛體問題中,可將剛體當作一個特殊的質點組(質量連續分佈,各質點間的距離保持不變)。將前面學過的關於質點組的動量定理,質心運動定理,角動量定理等用到這一特殊的質點組就可得到有關剛體的一些規律。特點
剛體在空間的位置,必須根據剛體中任一點的空間位置和剛體繞該點轉動時的位置(見剛體一般運動)來確定,所以剛體在空間有六個自由度。在很多情況下,固體在受力和運動過程中變形很小,基本上保持原來的大小和形狀不變。對此,人們提出了剛體這一理想模型。就是在任何情況下形狀和大小都不發生變化的物體,其特點是:在運動過程中,剛體的所有質元之間的距離始終保持不變。因此,構成剛體的質元只能以非常受限制的方式彼此相對運動。而且,作用在剛體各個部分之間的內力,在剛體的整體運動中不起作用。剛體是力學中的一個科學抽象概念,即理想模型。事實上任何物體受到外力,不可能不改變形狀。實際物體都不是真正的剛體。若物體本身的變化不影響整個運動過程,為使被研究的問題簡化,可將該物體當作剛體來處理而忽略物體的體積和形狀,這樣所得結果仍與實際情況相當符合。例如,物理天平的橫樑處於平衡狀態,橫樑在力的作用下產生的形變很小,各力矩的大小都幾乎不變。對於形變,實際是存在的,但可不予考慮。為此在研究天平橫樑平衡的問題時,可將橫樑當作剛體。在外力作用下,物體的形狀和大小(尺寸)保持不變,而且內部各部分相對位置保持恆定(沒有形變),這種理想物理模型稱之為剛體。剛體是個理想模型。如果物體的剛性足夠大,以致其中彈性波的傳播速度比該物體的運動速度大很多,從而可以認為彈性擾動的傳播是瞬時的,就可以把該物體當作剛體處理。在剛體問題中,可將剛體當作一個特殊的質點組(質量連續分佈,各質點間的距離保持不變)。將前面學過的關於質點組的動量定理,質心運動定理,角動量定理等用到這一特殊的質點組就可得到有關剛體的一些規律。特點 ①剛體上任意兩點的連線在平動中是平行且相等的!②剛體上任意質元的位置矢量不同,相差一恆矢量,但各質元的位移、速度和加速度卻相同。因此,常用“剛體的質心”來研究剛體的平動。
①剛體上任意兩點的連線在平動中是平行且相等的!②剛體上任意質元的位置矢量不同,相差一恆矢量,但各質元的位移、速度和加速度卻相同。因此,常用“剛體的質心”來研究剛體的平動。

剛體運動

剛體的轉動
描述物體或者一個力學系統的位置所需要的獨立坐標個數稱為該系統的自由度數。剛體運動不受任何約束時(即自由剛體) ,它的自由度為6個。
任意剛體兩點連線保持方向不變,各點的位移,速度,加速度相同,可當作質點來處理。
如果剛體在運動過程中,兩個坐標系的各坐標軸永遠相互平行,這種運動稱為平動。此時剛體上所有質點,都有相同的加速度。故剛體上任意一點的運動都可以代表整個剛體的運動,所以剛體平動時和質點的運動完全一樣,其自由度為3,可取c點的三個坐標xyz為廣義坐標,平動並不一定是直線運動,如圖所示的剛體就是一種平動,這裡每一個質點都作圓周運動但圖4.1(a)所示的鋼體運動就不再是一種平動,這裡每個質點都作圓周運動。但圖4.1(b)所示的剛體運動就不在是平動,因為在這種運動過程中,固定在剛體上的坐標軸並非始終保持和oxyz 的軸平行。
剛體上每點繞同一軸線做圓周運動,且轉軸空間位置及轉動方向保持不變。
如果剛體在運動過程中,至少有兩個質點保持不動,那麼將這兩個質點的連線取為兩個坐標系的一個公共坐標軸(z)軸,則剛體上各點都饒此軸作圓周運動,這種運動稱為定軸轉動。剛體在任一時刻的位置可用ox軸相對於ox.轉過的角度φ來確定,如圖4.2所示,其自由度為1,φ就是廣義坐標。
剛體的質心被限制在同一平面內,轉軸可平動,但始終垂直於該平面且通過質心。
如果剛體在運動過程中,剛體中任意一點始終在平行於某一固定平面的平面內運動,則稱為平面平行運動,簡稱平面運動,此時只須研究剛體中任一和固定平面平行的截面運動就夠了。
剛體上各點都在以某一定點為球心的球面上運動。
在運動過程中有一點永遠保持不動。我們可取這個固定點為上述兩個坐標系的公共原點,坐標軸之間的夾角則可以任一改變。可以證明,在這種情況下,剛體從一個初位置運動到任意一個新位置時,恆可通過三個獨立的角坐標來表示。設時,坐標系oxyz和ox.y.z.重合,如圖4.4(a);在時刻t,坐標系oxyz運動到一個新位置,如圖4.4(d)。這個運動可以看作三個獨立的轉動合成。首先,令oxyz平面繞oz.軸轉過一個角度φ,使ox軸達到圖4.4(d)中oxy平面和ox.y.平面的交線on的位置,變為ox'y'z'如圖4.4(b).交線on稱為節線。其次,使oy'z'平面繞節線on轉過角度θ,使坐標軸達到新位置ox"y"z",使oz"軸和圖4.4(d)中oz軸位置重合。最後,令ox"y"平面繞oz"軸轉過角度φ,使坐標軸達到圖4.4(d)中的最終位置。
上述φθØ三個角坐標稱為歐拉角,φ稱為進動角,θ稱為章動角,Ø稱為自轉角,這三個角度的變化範圍為:
。
從上面的討論可知,作定點轉動時,剛體在空間的任一位置可有三個歐拉角唯一確定,所以三個歐拉角就是剛體定點轉動的廣義坐標。
但是這種描述方法不是唯一的。例如我們也可以把剛體定點轉動看成是轉動軸oz方向可以任意變化的定軸轉動。要確定oz軸的方向,可用球坐標的余緯角θ和經度角φ來表示,在加上繞軸oz的轉角ψ,它們同樣可以唯一的確定剛體在空間的位置,也是廣義坐標,這三個角坐標和三個歐拉角並不完全一樣,其中θ和ψ是一樣的。但兩者的φ並不一樣。
平面運動與一般轉動的結合。
剛體作一般運動時,恆可以分解為平動和定點轉動兩部分,如圖4.5所示。平動部分可用c點的三個坐標x.y.z.描述,定點轉動部分可以用三個歐拉角φθψ描述。這6個坐標就是剛體作一般運動時的廣義坐標。