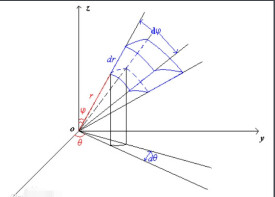
三重積分
三重積分
設三元函數f(x,y,z)在區域Ω上具有一階連續偏導數,將Ω任意分割為n個小區域,每個小區域的直徑記為ri(i=1,2,3.....n),體積記為Δδi,記||T||=maxri,在每個小區域內取點f(ξi,ηi,ζi),作和式Σf(ξi,ηi,ζi)Δδi,若該和式當||T||→0時的極限存在且唯一(即與Ω的分割和點的選取無關),則稱該極限為函數f(x,y,z)在區域Ω上的三重積分,記為∫∫∫f(x,y,z)dV,其中dV=dxdydz。
目錄
定義體積元素設三元函數z=f(x,y,z)定義在有界閉區域Ω上將區域Ω任意分成n個子域Δvi(i=123…,n)並以Δvi表示第i個子域的體積.在Δvi上任取一點(ξiηiζi)作和(n/i=1 Σ(ξiηiζi)Δvi).如果當各個子域的直徑中的最大值λ趨於零時,此和式的極限存在,則稱此極限為函數f(x,y,z)在區域Ω上的三重積分,記為∫∫∫f(x,y,z)dv,即Ω∫∫∫f(x,y,z)dv=lim λ→0 (n/i=1 Σf(ξi,ηi,ζi)Δvi),其中dv叫做體積元素。Ω術語∫∫∫‥‥‥三重積分號f(x,y,z)‥‥‥被積函數f(x,y,z)dv‥‥‥被積表達式dv‥‥‥體積元x,y,z‥‥‥積分變數Ω‥‥‥積分區域Σf(ξi,ηi,ζi)Δδi‥‥‥積分和
性質
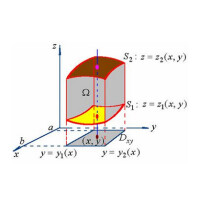
三重積分
計算方法
1直角坐標系法適用於被積區域Ω不含圓形的區域,且要注意積分表達式的轉換和積分上下限的表示方法⑴先一后二法投影法,先計算豎直方向上的一豎條積分,再計算底面的積分。①區域條件:對積分區域Ω無限制;②函數條件:對f(x,y,z)無限制。⑵先二后一法(截面法):先計算底面積分,再計算豎直方向上的積分。①區域條件:積分區域Ω為平面或其它曲面(不包括圓柱面、圓錐面、球面)所圍成;②函數條件:f(x,y,)僅為一個變數的函數。2柱面坐標法適用被積區域Ω的投影為圓時,依具體函數設定,如設x2+y2=a2,x=asinθ,y=acosθ①區域條件:積分區域Ω為圓柱形、圓錐形、球形或它們的組合;②函數條件:f(x,y,z)為含有與x2+y2(或另兩種形式)相關的項。3球面坐標系法適用於被積區域Ω包含球的一部分。①區域條件:積分區域為球形或球形的一部分,錐面也可以;②函數條件:f(x,y,z)含有與x2+y2+z2相關的項。
幾何意義
就是立體的質量。當積分函數為1時,就是其密度分佈均勻且為1,質量就等於其體積值。當積分函數不為1時,說明密度分佈不均勻。
應用
設Ω為空間有界閉區域,f(x,y,z)在Ω上連續;如果Ω關於xOy(或xOz或yOz)對稱,且f(x,y,z)關於z(或y或x)為奇函數,則:∫∫∫f(x,y,z)dv=0.Ω如果Ω關於xOy(或xOz或yOz)對稱,Ω1為Ω在相應的坐標面某一側部分,且f(x,y,z)關於z(或y或x)為偶函數,則:∫∫∫f(x,y,z)dV=2∫∫∫f(x,y,z)dvΩ Ω1如果Ω與Ω’關於平面y=x對稱,則:∫∫∫f(x,y,z)dv=∫∫∫f(y,x,z)dvΩ Ω’1