參數估計

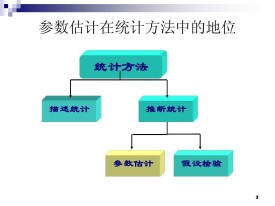
參數估計（parameter estimation）是根據從總體中抽取的樣本估計總體分佈中包含的未知參數的方法。人們常常需要根據手中的數據，分析或推斷數據反映的本質規律。即根據樣本數據如何選擇統計量去推斷總體的分佈或數字特徵等。統計推斷是數理統計研究的核心問題。所謂統計推斷是指根據樣本對總體分佈或分佈的數字特徵等作出合理的推斷。它是統計推斷的一種基本形式，是數理統計學的一個重要分支，分為點估計和區間估計兩部分。

在已知系統模型結構時，用系統的輸入和輸出數據計算系統模型參數的過程。18世紀末德國數學家C.F.高斯首先提出參數估計的方法，他用最小二乘法計算天體運行的軌道。20世紀60年代，隨著電子計算機的普及，參數估計有了飛速的發展。參數估計有多種方法，有最小二乘法、極大似然法、極大驗后法、最小風險法和極小化極大熵法等。在一定條件下，後面三個方法都與極大似然法相同。最基本的方法是最小二乘法和極大似然法。

用樣本矩估計總體矩，如用樣本均值估計總體均值。

為了選出使得模型輸出

與系統輸出

儘可能接近的參數估計值，可用模型與系統輸出的誤差的平方和來度量接近程度。使誤差平方和最小的參數值即為所求的估計值。

選擇參數

,使已知數據

在某種意義下最可能出現。某種意義是指似然函數

(

│

)最大，這裡

(

│

)是數據

的概率分佈函數。與最小二乘法不同的是，極大似然法需要已知這個概率分佈函數

(

│

)。在實踐中這是困難的，一般可假設

（

│

）是正態分佈函數，這時極大似然估計與最小二乘估計相同。

當估計值的數學期望等於參數真值時，參數估計就是無偏估計。當估計值是數據的線性函數時，參數估計就是線性估計。當估計值的均方差最小時，參數估計為一致最小均方誤差估計。若線性估計又是一致最小均方誤差估計，則稱為最優線性無偏估計。如果無偏估計值的方差達到克拉默-堯不等式的下界，則稱為有效估計值。若

（以概率1），則稱

為一致性估計值。在一定條件下，最小二乘估計是最優線性無偏估計，它的估計值是有效估計，而且是一致性估計。極大似然估計在一定條件下漸近有效，而且是一致的。

尋求最小二乘估計和極大似然估計的常用方法是將準則對參數

求導數，計算梯度，因而要使用最優化的方法：梯度法、變尺度法、單純形搜索法、牛頓-拉夫森法等。

為了減少計算量，便於在線估計參數，產生了許多遞推演演算法。一般是用遞推演演算法估計動態系統的參數。方法是：利用時刻

上的參數估計

、存儲向量

與時刻

+1上的輸入和輸出數據

和

，計算新的參數值

。每一步的計算時間比解一個線性代數方程組要少得多。

最小二乘法和極大似然法都有遞推形式，另外還有遞推廣義最小二乘法、遞推輔助變數法和遞推增廣最小二乘法等，都是遞推最小二乘法的改進形式，可以用來估計帶有色雜訊干擾的系統。此外，隨機逼近演演算法、卡爾曼濾波法和朗道遞推估計，是從不同的出發點得到的遞推參數估計法（見遞推估計演演算法），大多數遞推參數估計演演算法的一致性，即

（以概率1）,可以用鞅收斂性、常微分方程穩定性和超穩定性、正實性分別證明。

參數估計的方法很多，如何統一它們，如何在實踐中簡單有效地判斷它們的性質以及產生新的方法，都是有待進一步探討的問題。

P.艾克霍夫著，潘科炎、張永光等譯:《系統辨識──狀態與系統參數估計》，科學出版社，北京，1980。(P.Eykhoff，

, Wiley, London, 1974.)

區間估計是依據抽取的樣本，根據一定的正確度與精確度的要求，構造出適當的區間，作為總體分佈的未知參數或參數的函數的真值所在範圍的估計。例如人們常說的有百分之多少的把握保證某值在某個範圍內，即是區間估計的最簡單的應用。1934年統計學家J.奈曼創立了一種嚴格的區間估計理論。求置信區間常用的三種方法：①利用已知的抽樣分佈。②利用區間估計與假設檢驗的聯繫。③利用大樣本理論。