球面三角學
應用於測量學、航海等的幾何學
球面三角學是球面幾何學的一部分,主要在處理、發現和解釋多邊形(特別是三角形)在球面上的角與邊的聯繫和關聯。在天文學上的重要性是用於計算天體軌道和地球表面與太空航行時的天文導航。
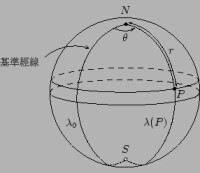
球面三角學
在球殼的表面,最短的距離是大圓上接近直線的弧線,也就是圓弧的圓心與球殼的球心是同一點。例如:地球上的子午線和赤道都是大圓。所謂行星表面的直線,就是球面上兩點之間最近距離的大圓弧線(如果你把自己拘束在球面上的直線上)。(參看:大地測量學)
在球面上,由大圓的弧所包圍的區域稱為球面多邊形,但要注意,不同於平面上的情形,在球面上’雙角’是可能存在的。(兩個弧夾出兩個角的三角形類似物)(可由剝橘子時剝下的橘子皮想像)
這些多邊形的邊長(弧長),可以利用球心角很方便的測定,將弧的兩端所對應的球心角乘上半徑便是邊長。要注意的是,這些角都必須用徑度量量度。.
因此,對一個球面三角形而言,是由他的弧長與球心角具體描述的,只是弧的長度是用徑度量標示。
值得注意的是,球面三角形的三個內角的和總是大於180°,但在平面上只有180°。超過180°的數值稱為球面剩餘E:,這些結餘給出了球面三角形的面積。確定這個值,球面剩餘必須以徑度量測定,表面積A依據球面的半徑和球面剩餘測量。
這是高斯-邦奈定理,這很明顯的顯示沒有相似的球面三角形(三角形有相同的角,但邊長和面積不同)。而在特殊的情況下,求的半徑為1,則球面三角形的面積。
要解球面幾何的問題,要點是能剖析出其中的直角三角形(三個角中有一個是90°),因為這樣就可以利用納皮爾的多邊形求解。
納皮爾的圓周顯示直角三角形的部份關聯性利用納皮爾多邊形(也稱為納皮爾圓周)的口訣可以很輕易的記住球面直角三角形的所有關聯性:以他們出現於球面三角形的順序,依照相鄰的邊角關係,依序將三角形的六個角寫在一個圈子內,也就是開始以一個角度開始,然後在它旁邊寫上相鄰的邊的弧角度,繼續再寫下下一個角度,最後結束成一個圓。然後刪除90°的角角度並且將它相鄰的弧角度替換成他們補角的數值(與原角弧度之和為90°)(也就是將a換成)。現在,這五個數組成了我們需要的納皮爾多邊形(納皮爾圓周),從這兒,可以得到每個角度的餘弦值。
球面三角形滿足球面餘弦定理這個恆等式的証明需要利用平面的餘弦定理和球面三角形的對角"C"延升的切線,而且,在小角度時可以引用平面幾何的公式。他也滿足並且有相似於平面形式的正弦定理。
http://xzf.2000y.net/mb/1/readnews.asp?newsid=525010