球面
三維幾何空間內理想的對稱體
球面是在三維幾何空間內理想的對稱體。
維空、歐幾里得、幾何學,球面被設定為是在 R空間中與一個定點距離為r的所有點的集合,此處r是一個正的實數,稱為半徑,固定的點稱為球心或中心,並且不屬於 球面的範圍。 r = 1是球的特例,稱為 單位球。
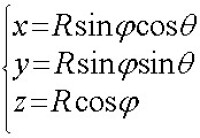
球面
(≤θ≤π,≤φ≤π)
在解析幾何,球是中心在(x0,y0,z0),半徑是r的所有點(x, y, z)的集合:
(x-x0)2+(y-y0)2+(z-z0)2=r2
球面
x=x0+r sinθcosφ
y=y0+r sinθsinφ
z=z0+r cosθ
(θ的取值範圍:0≤θ≤ n 和 -∏<φ≤∏)>
如果把球面看成地球時,參數φ就是地球上的緯度,θ就是 經度。經度和緯度也叫做地球上一點的 地理坐標。用平面去截球面,所得交線是圓。當平面通過球心時,在球面上截得的圓最大,稱為球面上的大圓,不過球心時截得的圓稱為小圓。小於半圓的弧稱為劣弧。把地球表面近似地看成一個球面時,經線就是從北極到南極的半個大圓,赤道是一個大圓,其他緯線都是小圓(圖2)。連接球面上兩點的所有曲線段之中以連接這兩點的大圓的劣弧為最短,稱為球面上兩點間的距離。因此在天空中的飛機和在大洋中的輪船,都儘可能沿大 圓弧航行。球面半徑為R時,球面面積為4πR^2,球的體積為(4/3)πR^3。
是到一點M(x,y,z)的距離為定長R的點的軌跡方程;x^2+y^2+z^2-2ax-2by-2cz+d=0
即(x-a)^2+(y-b)^2+(c-z)^2=a^2+b^2+c^2-d
當a^2+b^2+c^2-d>0時,表示一球面;當a^2+b^2+c^2-d=0時,表示一點(a,b,c);當a^2+b^2+c^2-d<0,表示虛球面。
