Prim

圖論中的演演算法之一

普里姆演演算法（Prim演演算法），圖論中的一種演演算法，可在加權連通圖裡搜索最小生成樹。意即由此演演算法搜索到的邊子集所構成的樹中，不但包括了連通圖裡的所有頂點（英語：Vertex (graph theory)），且其所有邊的權值之和亦為最小。該演演算法於1930年由捷克數學家沃伊捷赫·亞爾尼克（英語：Vojtěch Jarník）發現；並在1957年由美國計算機科學家羅伯特·普里姆（英語：Robert C. Prim）獨立發現；1959年，艾茲格·迪科斯徹再次發現了該演演算法。因此，在某些場合，普里姆演演算法又被稱為DJP演演算法、亞爾尼克演演算法或普里姆－亞爾尼克演演算法。

目錄
1簡介 2定義數據類型 3演算法描述
4時間複雜度 5圖例描述 6代碼

簡介

最小生成樹是數據結構中圖的一種重要應用，它的要求是從一個帶權無向完全圖中選擇n－1條邊並使這個圖仍然連通(也即得到了一棵生成樹),同時還要考慮使樹的權最小。
為了得到最小生成樹,人們設計了很多演演算法，最著名的有prim演演算法和kruskal演演算法。教材中介紹了prim演演算法，但是講得不夠詳細，理解起來比較困難，為了幫助大家更好的理解這一演演算法，本文對書中的內容作了進一步的細化，希望能對大家有所幫助。
假設V是圖中頂點的集合,E是圖中邊的集合,TE為最小生成樹中的邊的集合，則prim演演算法通過以下步驟可以得到最小生成樹:
1:初始化:U={u 0},TE={}。此步驟設立一個只有結點u 0的結點集U和一個空的邊集TE作為最小生成樹的初始行態，在隨後的演演算法執行中，這個行態會不斷的發生變化，直到得到最小生成樹為止。
2:在所有u∈U,v∈V－U的邊(u,v)∈E中，找一條權最小的邊(u 0,v 0)，將此邊加進集合TE中，並將此邊的非U中頂點加入U中。此步驟的功能是在邊集E中找一條邊，要求這條邊滿足以下條件：首先邊的兩個頂點要分別在頂點集合U和V－U中，其次邊的權要最小。找到這條邊以後，把這條邊放到邊集TE中，並把這條邊上不在U中的那個頂點加入到U中。這一步驟在演演算法中應執行多次，每執行一次，集合TE和U都將發生變化，分別增加一條邊和一個頂點，因此,TE和U是兩個動態的集合，這一點在理解演演算法時要密切注意。
3:如果U=V,則演演算法結束；否則重複步驟2。可以把本步驟看成循環終止條件。我們可以算出當U=V時，步驟2共執行了n－1次(設n為圖中頂點的數目),TE中也增加了n－1條邊，這n－1條邊就是需要求出的最小生成樹的邊。
了解了prim演演算法的基本思想以後，下面我們就可以看看具體的演演算法。
為了和教材保持一致，我們仍然規定：連通網用鄰接矩陣net表示，若兩個頂點之間不存在邊，其權值為計算機內允許最大值，否則為對應邊上的權值。

定義數據類型

type adjmatrix=array 【1．.n,1..n】 of real;
//定義一個n＊n的矩陣類型adjmatrix,以便存儲鄰接矩陣//
edge=record
beg,en:1..n;
length:real;
end;
//定義邊的存儲結構為edge,其中beg是邊的起點, en 是邊的終點,length是邊的權值//
treetype=array 【1..n－1】 of edge;
//定義一個基類型為edge的數組類型 treetype,其元素個數為n－1個//
var net:adjmatrix;
//定義一個adjmatrix類型的變數net,圖的鄰接矩陣就存放在net中//
tree:treetype;
//定義一個treetype類型的變數tree,tree中可以存放n－1條邊的信息，包括起點、終點及權值。在演演算法結束后，最小生成樹的n－1 條邊就存放在tree中//
演演算法如下(設n為構造的出發點)：
procedure prim(net:adjmatrix;var tree:treetype);
//過程首部。參數的含義是：值參數net傳遞圖的鄰接矩陣，變參tree指明最小生成樹的存放地址//
begin
for v:=1 to n－1 do
//此循環將頂點n與圖中其它n－1個頂點形成的n－1條邊存放在變數tree中//
【tree【v】.beg:=n;
tree【v】.en:=v;
tree【v】.length:=net【v】】
for k:=1 to n－1 do
//此循環執行演演算法思想中的步驟2,循環體每執行一次,TE中將增加一條邊，在演演算法中，這條增加的邊存放在變數tree中的第k個元素上，可以這樣認為,tree中從第1到第k號元素中存放了TE和U的信息。注意：在演演算法思想中我們特別提醒了TE和U的動態性，表現在演演算法中，這種動態性 體現在循環變數k的變化上。//
【min:=tree【k】.length;
for j:=k to n－1 do
if tree【j】.length
【min:=tree【j】.length;
m:=j;】
//上面兩條語句用於搜索權值最小的邊//
v:=tree【m】.en;
//此語句記錄剛加入TE中的邊的終點，也即即將加入U中的頂點//
edge:=tree【m】;
tree【m】:=tree【k】;
tree【k】:=edge;
//上面三句用於將剛找到的邊存儲到變數tree的第k號元素上//
for j:=k＋1 to n－1 do
//此循環用於更新tree中第k＋1到第n－1號元素。更新以後這些元素中的en子項是各不相同的，它們的全部就是集合V－U;beg子項則可以相同，但它們需滿足兩個條件：一是應屬於集合U;另一是beg子項和en子項行成的邊，在所有與頂點en聯繫的邊中權值應最小。//
【d:=net【v.tree【j】.en】;
if d
then 【tree【j】.length:=d;
tree【j】.beg:=v;】
】
】
for j:=1 to n－1 do
//此循環用於輸出最小生成樹//
writeln(tree【j】.beg,tree【j】.en,tree【j】.length);
end;
此演演算法的精妙之處在於對求權值最小的邊這一問題的分解(也正是由於這種分解，而導致了演演算法理解上的困難)。按照常規的思路，這一問題應該這樣解決：分別從集合V－U和U中取一頂點，從鄰接矩陣中找到這兩個頂點行成的邊的權值，設V－U中有m個頂點,U中有n個頂點，則需要找到m＊n個權值，在這m＊n個權值中，再查找權最小的邊。循環每執行一次，這一過程都應重複一次，相對來說計算量比較大。而本演演算法則利用了變數tree中第k＋1到第n－1號元素來存放到上一循環為止的一些比較結果，如以第k＋1號元素為例，其存放的是集合U中某一頂點到頂點tree.en的邊，這條邊是到該點的所有邊中權值最小的邊，所以，求權最小的邊這一問題，通過比較第k＋1號到第n－1號元素的權的大小就可以解決，每次循環只用比較n－k－2次即可，從而大大減小了計算量。

演演算法描述

1).輸入：一個加權連通圖，其中頂點集合為V，邊集合為E；
2).初始化：Vnew = {x}，其中x為集合V中的任一節點（起始點），Enew = {},為空；
3).重複下列操作，直到Vnew = V：
a.在集合E中選取權值最小的邊，其中u為集合Vnew中的元素，而v不在Vnew集合當中，並且v∈V（如果存在有多條滿足前述條件即具有相同權值的邊，則可任意選取其中之一）；
b.將v加入集合Vnew中，將邊加入集合Enew中；
4).輸出：使用集合Vnew和Enew來描述所得到的最小生成樹。

時間複雜度

最小邊、權的數據結構時間複雜度（總計）
鄰接矩陣、搜索O(V^2)
二叉堆（後文偽代碼中使用的數據結構）、鄰接表O((V + E) log(V)) = O(E log(V))
斐波那契堆、鄰接表O(E + V log(V))
通過鄰接矩陣圖表示的簡易實現中，找到所有最小權邊共需O（V）的運行時間。使用簡單的二叉堆與鄰接表來表示的話，普里姆演演算法的運行時間則可縮減為O(ElogV)，其中E為連通圖的邊數，V為頂點數。如果使用較為複雜的斐波那契堆，則可將運行時間進一步縮短為O(E+VlogV)，這在連通圖足夠密集時（當E滿足Ω（VlogV）條件時），可較顯著地提高運行速度。
這裡記頂點數v，邊數e
鄰接矩陣:O(v) 鄰接表:O(elog2v) 

圖例描述

圖例說明不可選可選已選（Vnew）
Prim
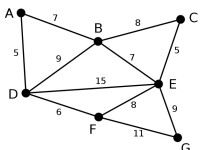Prim
此為原始的加權連通圖。每條邊一側的數字代表其權值。---
Prim
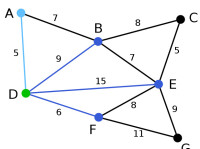Prim
頂點D被任意選為起始點。頂點A、B、E和F通過單條邊與D相連。A是距離D最近的頂點，因此將A及對應邊AD以高亮表示。C, GA, B, E, FD
Prim
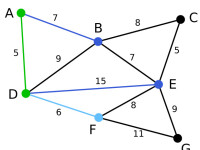Prim
下一個頂點為距離D或A最近的頂點。B距D為9，距A為7，E為15，F為6。因此，F距D或A最近，因此將頂點F與相應邊DF以高亮表示。C, GB, E, FA, D
Prim
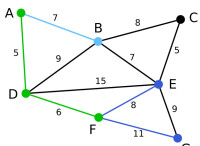Prim
演演算法繼續重複上面的步驟。距離A為7的頂點B被高亮表示。CB, E, GA, D, F
Prim
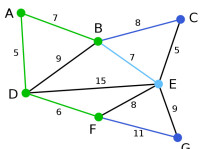Prim
在當前情況下，可以在C、E與G間進行選擇。C距B為8，E距B為7，G距F為11。點E最近，因此將頂點E與相應邊BE高亮表示。無C, E, GA, D, F, B
Prim
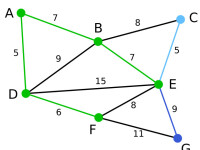Prim
這裡，可供選擇的頂點只有C和G。C距E為5，G距E為9，故選取C，並與邊EC一同高亮表示。無C, GA, D, F, B, E
Prim
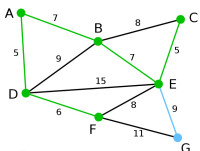Prim
頂點G是唯一剩下的頂點，它距F為11，距E為9，E最近，故高亮表示G及相應邊EG。無GA, D, F, B, E, C
Prim
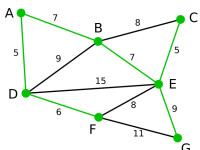Prim
所有頂點均已被選取，圖中綠色部分即為連通圖的最小生成樹。在此例中，最小生成樹的權值之和為39。無無A, D, F, B, E, C, G

代碼

PASCAL代碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
programprim;
const
map:array[1..6,1..6]ofinteger=((0,6,1,5,0,0),
(6,0,5,0,3,0),
(1,5,0,5,6,4),
(5,0,5,0,0,2),
(0,3,6,0,0,6),
(0,0,4,2,6,0));//樣例輸入
var
i,j,l:integer;
min,minn:longint;
f,d:array[1..6]ofinteger;
s:array[1..6,1..3]ofinteger;
v,p:setof1..6;
begin
l:=1;
p:=[];
v:=[];
fori:=2to6do
v:=v+[i];
p:=p+[1];
fori:=1to6do
f[i]:=1000;//還可以寫成filldword(f,sizeof(f)div2,1000)
f[1]:=0;
fori:=1to6dod[i]:=0;//還可以寫成fillchar(d,sizeof(d),0);
s[1,3]:=0;
fori:=1to5do
begin
min:=1000;
forj:=1to6do
begin
if(f[j]>map[l,j])and(jinv)and(map[l,j]<>0)then
begin
f[j]:=map[l,j];
d[j]:=l;
end;
if(f[j]0)then
begin
min:=f[j];
minn:=j;
end;
writeln(d[j]);
end;
f[minn]:=0;
v:=v-[minn];
p:=p+[minn];
s[i,1]:=d[minn];
l:=minn;
s[i,2]:=minn;
s[i,3]:=min;
end;
fori:=1to5dowrite(s[i,1],'to',s[i,2],'=',s[i,3],'-->');
readln;
end.
c代碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include
#include
#definemax1000000000;
inta[1001][1001],d[1001],p[1001];
intmain(){
inti,j,k,m,n,min,ans,t;
intx,y,z;
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++){
scanf("%d%d%d",&x,&y,&z);
a[x][y]=z;
a[y][x]=z;
}
for(i=1;i<=n;i++)
d[i]=1000000000;
d[1]=0;
for(i=2;i<=n;i++){
min=max;
for(j=1;j<=n;j++)
if(!p[j]&&min>d[j])
min=d[j];
t=j;
}
p[t]=j;
for(j=1;j<=n;j++)
if(a[t][j]=0&&d[j]>a[t][j]){
d[j]=a[t][j];
ans+=min;
}
printf("%d",ans);
return0;
}
C++代碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#define MAXN 1000
#define INF 1<<30
int closest[MAXN],lowcost[MAXN],m;//m為節點的個數
int G[MAXN][MAXN];//鄰接矩陣
int prim()
{
for(int i=0;i
{
lowcost[i] = INF;
}
for(int i=0;i
{
closest[i] = 0;
}
closest[0] = -1;//加入第一個點，-1表示該點在集合U中，否則在集合V中
int num = 0,ans = 0,e = 0;//e為最新加入集合的點
while (num < m-1)//加入m-1條邊
{
int micost = INF,miedge = -1;
for(int i=0;i
if(closest[i] != -1)
{
int temp = G[e][i];
if(temp < lowcost[i])
{
lowcost[i] = temp;
closest[i] = e;
}
if(lowcost[i] < micost)
micost = lowcost[miedge=i];
}
ans += micost;
closest[e = miedge] = -1;
num++;
}
return ans;
}

基本信息

中文名
普里姆演算法
外文名
Prim Algorithm
別名
最小生成樹演算法
運用領域
應用圖論知識的實際問題
提出者
沃伊捷赫·亞爾尼克（Vojtěch Jarník）
要求
從一個帶權無向完全圖中選擇n－1條邊並使這個圖仍然連通（也即得到了一棵生成樹）,同時還要考慮使樹的權最小
應用學科
計算機、數據結構、數學(圖論)
相關演算法
kruskal演算法
本質
一種應用
應用
資料庫
提出時間
1930年
  • 目錄