拉普拉斯方程
一種偏微分方程
拉普拉斯方程(Laplace's equation)又稱調和方程、位勢方程,是一種偏微分方程,因由法國數學家拉普拉斯首先提出而得名。
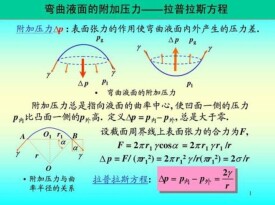
拉普拉斯方程表示液面曲率與液體表面壓強之間的關係的公式。
一個彎曲的表面稱為曲面,通常用相應的兩個曲率半徑來描述曲面,即在曲面上某點作垂直於表面的直線,再通過此線作一平面,此平面與曲面的截線為曲線,在該點與曲線相切的圓半徑稱為該曲線的曲率半徑。通過表面垂線並垂直於第一個平面再作第二個平面並與曲面相交,可得到第二條截線和它的曲率半徑,用 可表示出液體表面的彎曲情況。若液面是彎曲的,液體內部的壓強p1與液體外的壓強p2就會不同,在液面兩邊就會產生壓強差稱附加壓強,其數值與液面曲率大小有關,可表示為:,式中γ是液體表面張力係數,該公式稱為拉普拉斯方程。
其中稱為拉普拉斯運算元。
拉普拉斯方程的解稱為調和函數。
如果等號右邊是一個給定的函數,即:
則該方程稱為泊松方程。拉普拉斯方程和泊松方程是最簡單的橢圓型偏微分方程。偏微分運算元(可以在任意維空間中定義這樣的運算元)稱為拉普拉斯運算元,英文是Laplace operator或簡稱作Laplacian。
稱為調和函數,此函數在方程成立的區域內是解析的。任意兩個函數,如果它們都滿足拉普拉斯方程(或任意線性微分方程),這兩個函數之和(或任意形式的線性組合)同樣滿足前述方程。這種非常有用的性質稱為疊加原理。可以根據該原理將複雜問題的已知簡單特解組合起來,構造適用面更廣的通解。
兩個自變數的拉普拉斯方程具有以下形式:
解析函數的實部和虛部均滿足拉普拉斯方程。
拉普拉斯,1749年3月23日生於法國西北部卡爾瓦多斯的博蒙昂諾日,曾任巴黎軍事學院數學教授。1795年任巴黎綜合工科學校教授,后又在高等師範學校任教授。1799年他還擔任過法國經度局局長,並在拿破崙政府中任過6個星期的內政部長。1816年被選為法蘭西學院院士,1817年任該院院長。1827年3月5日卒於巴黎。拉普拉斯在研究天體問題的過程中,創造和發展了許多數學的方法,以他的名字命名的拉普拉斯變換、拉普拉斯定理和拉普拉斯方程,在科學技術的各個領域有著廣泛的應用。
拉普拉斯曾任拿破崙的老師,所以和拿破崙結下不解之緣。拉普拉斯在數學上是個大師,在政治上是個小人物、牆頭草,總是效忠於得勢的一邊,被人看不起,拿破崙曾譏笑他把無窮小量的精神帶到內閣里。在席捲法國的政治變動中,包括拿破崙的興起和衰落,沒有顯著地打斷他的工作。儘管他是個曾染指政治的人,但他的威望以及他將數學應用于軍事問題的才能保護了他,同時也歸功於他顯示出的一種並不值得佩服的在政治態度方面見風使舵的能力。