具體運算階段
具體運算階段
具體運算階段,是皮亞傑認知發展理論中認知發展4個階段中的第三個,在前運算階段之後,從7歲到12歲,表現為邏輯的適當使用。該階段的思維有兩個主要特點:①守恆性。兒童能從一個概念的各種具體變化中抓住實質或本質的東西;②能進行群集運算。群集運算包括組合性、逆向性、結合性、同一性、重複性五個方面。具體運算思維一般還離不開具體事物的支持,而且這些運算還是零散的,還不能組成一個結構的整體、一個完整的系統。
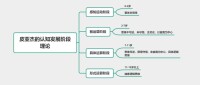
具體運算階段
可逆性——兒童理解數字或物體改變后,可以回到原來的狀態。
守恆——懂得條目的數量或長度與物體或條目的排列或外觀無關。
連續性——根據大小、形狀或其他特徵排列物體的能力。
分類——命名並根據外觀、大小或其他特徵給一批物體進行分類的能力,包括一類物體可以包括另一類的觀念。
一、運算指一種內化了的動作,即能在頭腦中進行的思維活動。
二、運算是一種可逆的動作。如1+1=2,它的相反就是2-1=1。
三、運算具有一種守恆性,當一個運算在變換時,體系中總有幾個保持不變的特點。
四、系統性。運算格式是一個系統,不能單獨進行,要協調成為一個整體。具體運算階段有兩個顯著特點:1.獲得了守恆性;2.群集結構的形成。
運算階段和前運算階段的主要區別:1.運算階段依靠概念進行,前運算階段依靠表象進行。2.運算階段有可逆性,前運算階段沒有。3.運算階段具有守恆概念,前運算階段沒有。4.前運算階段是自我中心的,運算階段逐漸非中心化。5.前運算階段是不靈活的,具有固定性、刻板性或獃滯性。運算思維具有靈活性。
具體運算階段和形式運算階段:
1.具體運算思維還不能離開具體事物的表象,要以具體表象為支柱。
2.具體運算還不是一個完善的整體結構,這種運算還是零散的。
