非奇非偶函數 如果對於函數定義域內的任意一個x,若f(-x)=-f(x)(奇函數)或f(-x)=f(x)(偶函數)都不能成立,那麼函數f(x)既不是奇函數又不是偶函數,稱為非奇非偶函數。判斷函數奇偶性的第一步就是判斷函數的定義域是否關於數零對稱(這裡很多人不能理解,網上也經常有很多錯誤的實例,定義域應該關於數零對稱,並不是關於原點對稱,也不是關於y軸對稱),如果定義域不關於數零對稱那麼顯然是非奇非偶函數。
當然,如果和都能成立,
那麼函數f(x)既是奇函數又是偶函數。
非奇非偶函數與既奇又偶函數的區別:
奇函數:
偶函數:
既奇又偶函數:
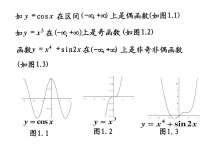
非奇非偶函數
和
非奇非偶函數:
存在X1,X2,使得:
f(-X1)不等於f(X1)
f(-X2)不等於-f(X2)
當然,定義域沒有與原點對稱的函數也是非奇非偶函數。
奇函數:
偶函數:
既奇又偶函數:
和
在平面直角坐標系中,既不關於原點對稱又不關於y軸對稱。