發酵動力學
發酵動力學
發酵動力學 是研究各種環境因素與微生物代謝活動之間的相互作用隨時間變化的規律的科學。
fermentation kinetics
生化反應工程的基礎內容之一,以研究發酵過程的反應速率和環境因素對速率的影響為主要內容。通過發酵動力學的研究,可進一步了解微生物的生理特徵,菌體生長和產物形成的合適條件,以及各種發酵參數之間的關係,為發酵過程的工藝控制、發酵罐的設計放大和用計算機對發酵過程的控制創造條件。
研究發酵過程中菌的生長速率、培養基的消耗速率和產品形成速率的相互作用和隨時間變化的規律。
它為發酵過程的控制、小罐試驗數據的放大以及從分批發酵過渡到半連續發酵和連續發酵提供了理論基礎。
發酵動力學也是計算機模擬發酵過程研究及發酵過程計算機在線控制的基礎。
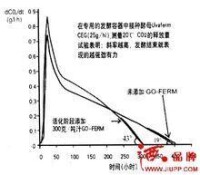
發酵動力學
菌體生長可分遲滯、對數、減速、靜止、衰退等五個時期。其中菌體的主要生長期是對數期,它的特點是:
隨著基質濃度繼續下降,菌體的衰老死亡逐步與生長平衡以至超過生長,也即進入靜止和衰退期。

發酵動力學
μm為最大比生長速率, 即不因基質濃度變化而改變的最大μ值;Ks為飽和常數,即在數量上相當於時的S值。Ks值愈小,說明在低基質濃度範圍中,S對μ愈為敏感,而保持μm的臨界S值愈低。在一般情況下,當時,當時,。產物的形成常與菌體的生長或濃度有關.α、β為常數;qP為比產物形成速率。在限制性基質的消耗和菌體生長間常用下式表示:式中YG為菌體得率常數;則為單純用於合成單位菌體所耗用的基質量;m為維持係數,即單位菌體、單位時間內耗用於菌體維持生命活動的基質量;qS為比限制性基質消耗速率。
若在菌體生長時還伴有產物形成,則或
式中為產物得率係數;則為單純用於合成單位產物所耗用的基質量。

