熱力學第零定律

熱力學第零定律的重要性在於它給出了溫度的定義和溫度的測量方法。定律中所說的熱力學系統是指由大量分子、原子組成的物體或物體系。它為建立溫度概念提供了實驗基礎。這個定律反映出：處在同一熱平衡狀態的所有的熱力學系統都具有一個共同的宏觀特徵，這一特徵是由這些互為熱平衡系統的狀態所決定的一個數值相等的狀態函數，這個狀態函數被定義為溫度。而溫度相等是熱平衡之必要的條件。

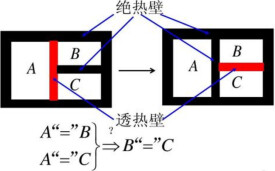
熱力學中以熱平衡概念為基礎對溫度作出定義的定律。通常表述為：與第三個系統處於熱平衡狀態的兩個系統之間，必定處於熱平衡狀態。圖中A熱力學第零定律示意圖、B熱力學第零定律示意圖、C熱力學第零定律示意圖為3個質量和組成固定，且與外界完全隔絕的熱力系統。將其中的B、C用絕熱壁隔開，同時使它們分別與A發生熱接觸。待A與B和A與C都達到熱平衡時，再使B與C發生熱接觸。這時B和C的熱力狀態不再變化，這表明它們之間在熱性質方面也已達到平衡。第零定律表明，一切互為熱平衡的系統具有一個數值上相等的共同的宏觀性質── 溫度。溫度計所以能夠測定物體溫度正是依據這個原理。

處於熱力學平衡狀態的所有物質均具有某一共同的宏觀物理性質。

熱力學第零定律用來作為進行體系測量的基本依據，其重要性在於它說明了溫度的定義和溫度的測量方法。表述如下：

1.可以通過使兩個體系相接觸，並觀察這兩個體系的性質是否發生變化而判斷這兩個體系是否已經達到熱平衡。

2.當外界條件不發生變化時，已經達成熱平衡狀態的體系，其內部的溫度是均勻分佈的，並具有確定不變的溫度值。

3.一切互為平衡的體系具有相同的溫度，所以一個體系的溫度可以通過另一個與之平衡的體系的溫度來表示，也可以通過第三個體系的溫度來表示。

ps：初中物理公式，熱學部分：1，吸熱：;2,放熱：;3,熱力學溫度：

第零定律比起其他任何定律更為基本，但直到二十世紀三十年代前一直都未有察覺到有需要把這種現象以定律的形式表達。第零定律是由英國物理學家拉爾夫·福勒於1939年正式提出，比熱力學第一定律和熱力學第二定律晚了80餘年，但是第零定律是後面幾個定律的基礎，所以叫做熱力學第零定律。

一個熱平衡系統的宏觀物理性質（壓強、溫度、體積等）都不會隨時間而改變。一杯放在餐桌上的熱咖啡，由於咖啡正在冷卻，所以這杯咖啡與外界環境並非處於平衡狀態。當咖啡不再降溫時，它的溫度就相當於室溫，並且與外界環境處於平衡狀態。

兩個互相處於平衡狀態的系統會滿足以下條件：

● ● 兩者各自處於平衡狀態；

● ● 兩者在可以交換熱量的情況下，仍然保持平衡狀態。進而推廣之，如果能夠肯定兩個系統在可以交換熱量的情況下物理性質也不會發生變化時，即使不容許兩個系統交換熱量，也可以肯定互為平衡狀態。

因此，熱平衡是熱力學系統之間的一種關係。數學上，第零定律表示這是一種等價關係。（技術上，需要同時包括系統自己亦都處於熱平衡。）

第零定律是在不考慮引力場作用的情況下得出的，物質（特別是氣體物質）在引力場中會自發產生一定的溫度梯度。如果有封閉兩個容器分別裝有氫氣和氧氣，由於它們的分子量不同，它們在引力場中的溫度梯度也不相同。如果最低處它們之間可交換熱量，溫度達到相同，但由於兩種氣體溫度梯度不同，則在高處溫度就不相同，也即不平衡。因此第零定律不適用引力場存在的情形。這與限定第二類永動機不成立的第二定律類似。

第零定律經常被認為可以建立一個溫度函數；更隨便的說法是可以製造溫度計。而這個問題是其中一個熱力學和統計力學哲學的題目。

在熱力學變數的函數空間之中，恆溫的部分會成為一塊面並會為附近的面提供自然秩序。之後，該面會簡單建立一個可以提供連續狀態順序的總體溫度函數。該恆溫面的維度是熱力學變數的總數減一（例如對於有三個熱力學變數 P、V、n 的理想氣體，其恆溫面是塊二維面）。按此定義的溫度實際上未必如攝氏溫度尺般，而是一個函數。

以理想氣體為例，若兩團氣體是處於熱平衡，則：

Pi 是第 i 個系統的壓強Vi 是第 i 個系統的體積Ni 是第 i 個系統的數量（摩爾數或者原子數目）面 定義了所有相同溫度的面，一個常見方法來標籤這些面是令 ，R 是一個常數而溫度 T 可以由此定義。經定義后，這些系統可用作溫度計來較准其他系統。

一個簡單例子可以說明為什麼需要到第零定律。如前所述，當兩個系統間有小量廣延量交換時（如微觀波動）而兩者的總能量不變時（能量減少不能逆轉），此兩個系統即處於平衡。

簡單起見，N個系統與宇宙的其他部分絕應隔離，每一個系統的體積與組成都保持恆定，而各個系統之間都只能交換熱量（熵）。此例子的結果可直接延伸至體積或積量的交換。

熱力學第一與第二定律的結合把總能量波動 與第 i個系統的溫度 及熵的波動 聯繫成：

與宇宙其他部分絕熱隔離，N個系統熵的總和必須為零。

換句話說，熵只能在 N個系統之間交換。這個限制可以用來重寫總能量波動的表達式成：

 是N個系統中任何一個系統 j的溫度。最後到達平衡時，總能量波動必須為零，因此：

 這條方程可被設想成反對稱矩陣與熵波動矢量之乘積為零。若要令一個非零解存在，則：

無論是那一個 j的選擇，由組成之矩陣的行列式值必定歸零。

但是，根據雅可比定理，一個反對稱矩陣若N為奇數時，則其行列式值必為零；而若N為偶數時，則每一項必須為零以令行列式值為零，亦即各個系統處於平衡狀態。此結果顯示，奇數數目的系統必定處於平衡狀態，而各系統的溫度和熵波動則可以忽略不計；熵波動存在時，只有偶數數目的系統才須要各系統的溫度相等以達致平衡狀態。

熱力學第零定律解決了此奇偶矛盾。考慮N個系統中的任何三個互為平衡的系統，其中一個就系統可以按照第零定律而被忽略。因此，一個奇數數數的系統就可以約簡成一個偶數數目的系統。此推導使為平衡的必須條例。

相同結果，可以應用到任何廣延量中的波動如體積（相同壓強）、或質量（相同化勢）。因而，第零定律的所涉及的就不單隻是溫度罷了。

總的來說，第零定律打破了第一定律和第二定律內的某種反對稱性。