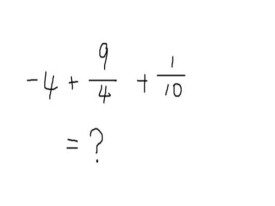負分數
小於0的分數
分數（來自拉丁語，“破碎”）代表整體的一部分，或更一般地，任何數量相等的部分。當在日常英語中說話時，分數描述了一定大小的部分，例如半數，八分之五，四分之三。分子和分母也用於不常見的分數，包括複合分數，複數分數和混合數字。小於0的分數即為負分數負分數加減法的運算規律和正負整數加減法的運算規律完全相同，即：同號兩數相加，取相同的符號，並把絕對值相加。異號兩數相加，取較大的加數的符號，並用較大的絕對值減去較小的絕對值。
小於0的分數即為負分數
或是可以化成分數的負有限小數和負無限循環小數。
對於負分數的加減運算，先確定和、差的符號，再轉化為正分數的加減運算。
減去一個數等於加上這個數的相反數。互為相反數的兩個數相加為零。
1.判斷一個數是否是負分數時，一定要依據其最原始的形態來判斷。
例：是負分數，因為雖然約分后等於－2，但是意義是完全不一樣的。分數里又有真、假分數。真分數又包括一般真分數和最簡真分數。 是負的一般真分數，它是分數。但不可以說它是整數。
2.因為所有的數都可以寫成該數比1的形式，所以一般認為形如負一分之幾的數不屬於負分數。
3.不等式中有分式時要考慮它的符號。
在歷史上，分數幾乎與自然數一樣古老。早在人類文化發明的初期，由於進行測量和均分的需要，所以人們引入並使用了分數。
在許多民族的古代文獻中都有關於分數的記載和各種不同的分數制度。早在公元前2100多年，古代巴比倫人（現處伊拉克一帶）就使用了分母是60的分數。
我國春秋時代（公元前770年～前476年）的《左傳》中，規定了諸侯的都城大小：最大不可超過周文王國都的三分之一，中等的不可超過五分之一，小的不可超過九分之一。秦始皇時代的曆法規定：一年的天數為三百六十五又四分之一。這說明：分數在我國很早就出現了，並且用於社會生產和生活。
人類歷史上最早產生的數是自然數（非負整數），以後在度量和平均分時往往不能正好得到整數的結果，這樣就產生了分數。
用一個作標準的量（度量單位）去度量另一個量，只有當量若干次正好量盡的時候，才可以用一個整數來表示度量的結果。如果量若干次不能正好量盡，有兩種情況：
例如，用b作標準去量a：
一種情況是把b分成n等份，用其中的一份作為新的度量單位去度量a，量m次正好量盡，就表示a含有把b分成n等份以後的m個等份。例如，把b分成4等份，用其中的一份去量a，量9次正好量盡．在這種情況下，不能用一個整數表示用b去度量a的結果，就必須引進一種新的數—分數來表示度量的結果。
另一種情況是無論把b分成幾等份，用其中的一份作為新的度量a，都不能恰好量盡（如用圓的直徑去量同一圓的周長）。在這種情況下，就需要引進一種新的數-無理數。在整數除法中，兩個數相除，有時不能得到整數商。為了使除法運算總可以施行，也需要引進新的一種數-分數。
綜上所述，分數是在實際度量和均分中產生的。
負分數
定義：小於0的分數或是可化成分數的 負有限小數或負無限循環小數。
定義：把單位“1”或整體“1”平均分成若干份，表示這樣的一份或幾份的數叫做分數。分母表示把一個物體平均分成幾份，分子是表示這樣幾份的數。把1平均分成分母份，表示這樣的分子份。分子在上分母在下，也可以把它當做除法來看，用分子除以分母，相反除法也可以改為用分數表示。
最簡分數
定義：分子和分母的公因數只有1。
定義：整數和分數統稱為有理數，任何一個有理數都可以寫成分數m/n（m，n都是整數，且n≠0）的形式。
有理數包括：
(1)自然數：數0，1，2，3，……叫做自然數.
(2)正整數：+1，+2，+3，……叫做正整數。
(3）負整數：－1，－2，－3，……叫做負整數。
(4）整數：正整數、0、負整數統稱為整數。
(5）分數：正分數、負分數統稱為分數。
(6）奇數：不能被2整除的整數叫做奇數。如-3，-1，1，5等。所有的奇數都可用2n-1或2n+1表示，n為整數。
(7）偶數：能被2整除的整數叫做偶數。如-2，0，4，8等。所有的偶數都可用2n表示，n為整數。
(8）質數：如果一個大於1的整數，除了1和它本身外，沒有其他因數，這個數就稱為質數，又稱素數，如2，3，11，13等。2是最小的質數。
(9）合數：如果一個大於1的整數，除了1和它本身外，還有其他因數，這個數就稱為合數，如4，6，9，15等。4是最小的合數。一個合數至少有3個因數。
(10）互質數：如果兩個正整數，除了1以外沒有其他公因數，這兩個整數稱為互質數，如2和5，7和13等。
……
如都是有理數。
無限不循環小數稱之為無理數（例如：圓周率π），不屬於有理數，而無限循環小數如3.333……則屬於有理數。
基本信息
- 中文名
- 負分數
- 外文名
- Negative score
- 易錯點
- 判斷一個數是否是負分數
- 分數定義
- 表示整體的一份幾份的數叫做分數
- 運算規律
- 加減法的運算規律完全相同
- 定義
- 小於0的分數即為負分數