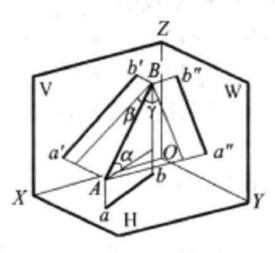
一般位置直線
與三個投影面都傾斜的直線
對三個投影面無平行、垂直關係,而對三個投影面都傾斜的直線稱為一般位置直線。直線與H,V,W三個投影面的夾角一般分別用α,β,γ表示。一般位置直線的各投影與投影軸傾斜且不能反映AB與各投影面的夾角,且三個投影均為縮短了的直線段。
在三投影面體系中,與三個投影面都傾斜的直線稱為 一般位置直線(圖1)。一般位置直線段的投影規律是:三個投影均為縮短了的直線段。三個投影均不反映直線段與投影面夾角的實際大小。
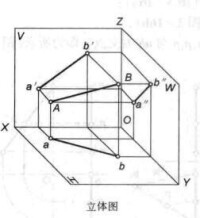
圖1(a)
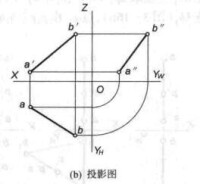
圖1(b)
一般位置直線的投影特性(如圖2、3):
各投影與投影軸傾斜且不能反映AB與各投影面的夾角。
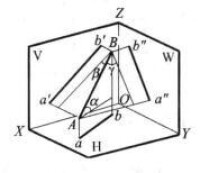
圖2
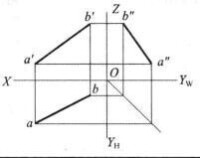
圖3
從一般位置直線投影特性可知,直線AB的三個投影均小於AB,不能反映直線AB的實長及它們對各投影面的傾角,但我們可用圖解法來求出其實長和傾角,具體作法如圖4所示。
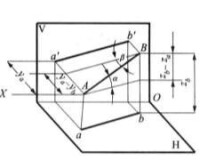
圖4(a) 軸測圖
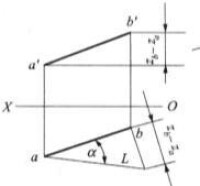
圖4(b)求實長L和α角
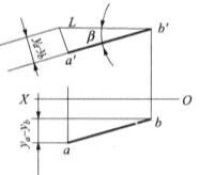
圖4(c)求實長L和β角
在圖4 (a)中,平行四邊形ABba垂直於H面,如過點A在此平面內作一直線平行於ab,則在此平面內形成一直角三角形,其斜邊即為此直角三角形的實長AB,直角底邊平行且等於ab,而其另一直角邊則為A和B兩點的Z坐標差。如在投影圖上已知直線AB的水平投影ab以及直線AB兩點的Z坐標差(此差可在正面投影中量得),則可以通過作一直角三角形而求出實長L及α角。α是直線AB與它在H面上的正投影間的夾角。因此,必是直線AB與H面的夾角,如圖4(b)所示。這就是通常所說的用 直角三角形法求直線的實長與傾角的方法,也是利用投影來圖解空間幾何問題度量的一個例子。
同理,如圖4(c)所示,可求出直線AB的實長L及其與V面的夾角β。在子面體系中,還可利用點A和點B的Z坐標差作一直角三角形,而求出直線AB的實長L及其與W面的傾角γ。
(1)以直線AB的水平投影ab為直角底邊,以點A和點B的Z坐標差為直角邊所組成的直角三角形,其斜邊即為AB的實長L,L與ab的夾角即為AB與H面的夾角α。
(2)以直線AB的正面投影a'b’為直角底邊,以點A和點B的Y坐標差為直角邊所組成的直角三角形,其斜邊即為AB的實長L,L與a'b’的夾角即為AB與V面的夾角β。
(3)以直線AB的側面投影a''b''為直角底邊,以點A和點B的X坐標差為直角邊所組成的直角三角形,其斜邊即為AB的實長L,L與a''b''的夾角即為AB與W面的夾角γ。