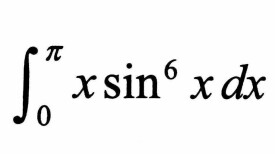定積分
函數f(x)在區間[a,b]上的積分和的極限
定積分是積分的一種,是函數f(x)在區間[a,b]上的積分和的極限。這裡應注意定積分與不定積分之間的關係:若定積分存在,則它是一個具體的數值(曲邊梯形的面積),而不定積分是一個函數表達式,它們僅僅在數學上有一個計算關係(牛頓-萊布尼茨公式),其它一點關係都沒有!一個函數,可以存在不定積分,而不存在定積分,也可以存在定積分,而不存在不定積分。一個連續函數,一定存在定積分和不定積分;若只有有限個間斷點,則定積分存在;若有跳躍間斷點,則原函數一定不存在,即不定積分一定不存在。
不定積分(Indefinite integral)
即已知導數求原函數。若F′(x)=f(x),那麼[F(x)+C]′=f(x).(C∈R,C為常數).也就是說,把f(x)積分,不一定能得到F(x),因為F(x)+C的導數也是f(x)(C是任意常數)。所以f(x)積分的結果有無數個,是不確定的。所以一律用F(x)+C代替,這就稱為不定積分。即如果一個導數有原函數,那麼它就有無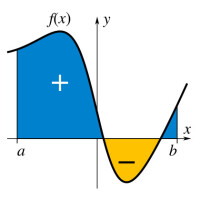 限多個原函數。
限多個原函數。

定積分
定積分(definite integral)
定積分就是求函數f(X)在區間[a,b]中的圖像包圍的面積。即由 y=0,x=a,x=b,y=f(X)所圍成圖形的面積。這個圖形稱為曲邊梯形,特例是曲邊三角形。
設函數f(x)在區間[a,b]上連續,將區間[a,b]分成n個子區間[x0,x1], (x1,x2], (x2,x3], …, (xn-1,xn],其中x0=a,xn=b。可知各區間的長度依次是:△x1=x1-x0,在每個子區間(xi-1,xi]中任取一點ξi(1,2,...,n),作和式。該和式叫做積分和,設λ=max{△x1, △x2, …, △xn}(即λ是最大的區間長度),如果當λ→0時,積分和的極限存在,則這個極限叫做函數f(x) 在區間[a,b]的定積分,記為,並稱函數f(x)在區間[a,b]上可積。
其中:a叫做積分下限,b叫做積分上限,區間[a, b]叫做積分區間,函數f(x)叫做被積函數,x叫做積分變數,f(x)dx 叫做被積表達式,∫ 叫做積分號。
之所以稱其為定積分,是因為它積分后得出的值是確定的,是一個常數,而不是一個函數。
根據上述定義,若函數f(x)在區間[a,b]上可積分,則有n等分的特殊分法:
特別注意,根據上述表達式有,當[a,b]區間恰好為[0,1]區間時,則[0,1]區間積分表達式為:
1、當a=b時,
2、當a>b時,
3、常數可以提到積分號前。
4、代數和的積分等於積分的代數和。
5、定積分的可加性:如果積分區間[a,b]被c分為兩個子區間[a,c]與[c,b]則有
又由於性質2,若f(x)在區間D上可積,區間D中任意c(可以不在區間[a,b]上)滿足條件。
6、如果在區間[a,b]上,f(x)≥0,則
7、積分中值定理:設f(x)在[a,b]上連續,則至少存在一點ε在(a,b)內使
如果
(1) ;
(2)x=ψ(t)在[α,β]上單值、可導;
(3)當α≤t≤β時,a≤ψ(t)≤b,且ψ(α)=a,ψ(β)=b,則
設u=u(x),v=v(x)均在區間[a,b]上可導,且u′,v′∈R([a,b]),則有分部積分公式:
定積分是把函數在某個區間上的圖象[a,b]分成n份,用平行於y軸的直線把其分割成無數個矩形,再求當n→+∞時所有這些矩形面積的和。習慣上,人們用等差級數分點,即相鄰兩端點的間距Δx是相等的。但是必須指出,即使Δx不相等,積分值仍然相同。假設這些“矩形面積和”
那麼當n→+∞時,Δx的最大值趨於0,所以所有的Δx趨於0,所以S仍然趨於積分值.
利用這個規律,在了解牛頓-萊布尼茲公式之前,便可以對某些函數進行積分。
例如:證明對於函數 有
證明:選擇等比級數來分點,令公比
且
“矩形面積和”為
提取,則有
利用等比級數公式,得到
其中 設 令,則
令n增加,則s,q都趨於1,因而N的極限為。
可以看到,定積分的本質是把圖象無限細分,再累加起來,而積分的本質是求一個導函數的原函數。它們看起來沒有任何的聯繫,那麼為什麼定積分要寫成積分的形式呢?
一般定理
定理1:設f(x)在區間[a,b]上連續,則f(x)在[a,b]上可積。
定理2:設f(x)區間[a,b]上有界,且只有有限個間斷點,則f(x)在[a,b]上可積。
定理3:設f(x)在區間[a,b]上單調,則f(x)在[a,b]上可積。
牛頓-萊布尼茨公式
定積分與不定積分看起來風馬牛不相及,但是由於一個數學上重要的理論的支撐,使得它們有了本質的密切關係。把一個圖形無限細分再累加,這似乎是不可能的事情,但是由於這個理論,可以轉化為計算積分。這個重要理論就是大名鼎鼎的牛頓-萊布尼茲公式,它的內容是:
如果f(x)是[a,b]上的連續函數,並且有F′(x)=f(x),那麼
用文字表述為:一個定積分式的值,就是原函數在上限的值與原函數在下限的值的差。
正因為這個理論,揭示了積分與黎曼積分本質的聯繫,可見其在微積分學以至更高等的數學上的重要地位,因此,牛頓-萊布尼茲公式也被稱作微積分基本定理。
解決求曲邊圖形的面積問題
例:求由拋物線 與直線 圍成的平面圖形D的面積S.
求變速直線運動的路程
做變速直線運動的物體經過的路程s,等於其速度函數v=v(t) (v(t)≥0)在時間區間[a,b]上的定積分。
變力做功
某物體在變力F=F(x)的作用下,在位移區間[a,b]上做的功等於F=F(x)在[a,b]上的定積分。(見圖冊“應用”)
數列求和的極限
若函數在[a,b]上連續,則有:
若函數在[a,b]上連續,則有:
若函數在[0,1]上連續,則有:
以上三個結論。