不定積分

根據牛頓-萊布尼茨公式，許多函數的定積分的計算就可以簡便地通過求不定積分來進行。這裡要注意不定積分與定積分之間的關係：定積分是一個數，而不定積分是一個表達式，它們僅僅是數學上有一個計算關係。一個函數，可以存在不定積分，而不存在定積分，也可以存在定積分，而沒有不定積分。連續函數，一定存在定積分和不定積分；若在有限區間[a,b]上只有有限個間斷點且函數有界，則定積分存在；若有跳躍、可去、無窮間斷點，則原函數一定不存在，即不定積分一定不存在。

1、函數的和的不定積分等於各個函數的不定積分的和；即：設函數及的原函數存在，則

2、求不定積分時，被積函數中的常數因子可以提到積分號外面來。即：設函數的原函數存在，非零常數，則

設F(x)是函數f(x)的一個原函數，我們把函數f(x)的所有原函數F(x)+ C(其中，C為任意常數）叫做函數f(x)的不定積分，又叫做函數f(x)的反導數，記作∫f(x)dx或者∫f（高等微積分中常省去dx），即。其中∫叫做積分號，f(x)叫做被積函數，x叫做積分變數，f(x)dx叫做被積式，C叫做積分常數或積分常量，求已知函數的不定積分的過程叫做對這個函數進行不定積分。

由定義可知：

求函數f(x)的不定積分，就是要求出f(x)的所有的原函數，由原函數的性質可知，只要求出函數f(x)的一個原函數，再加上任意的常數C就得到函數f(x)的不定積分。

註：以下的C都是指任意積分常數。

1、 ，a是常數

2、 ，其中a為常數，且a ≠ -1

3、

4、

5、 ，其中a > 0 ，且a ≠ 1

6、

7、

8、

9、

10、

11、

12、

13、

14、

15、

全體原函數之間只差任意常數C

證明：如果f(x)在區間I上有原函數，即有一個函數F(x)使對任意x∈I，都有F'(x)=f(x)，那麼對任何常數顯然也有[F(x)+C]'=f(x).即對任何常數C，函數F(x)+C也是f(x)的原函數。這說明如果f(x)有一個原函數，那麼f(x)就有無限多個原函數。

設G(x)是f(x)的另一個原函數，即。於是由於在一個區間上導數恆為零的函數必為常數，所以(C‘為某個常數)。

這表明G(x)與F(x)只差一個常數。因此，當C為任意常數時，表達式F(x)+C就可以表示f(x)的任意一個原函數。也就是說f(x)的全體原函數所組成的集合就是函數族。

由此可知，如果F(x)是f(x)在區間I上的一個原函數，那麼就是f(x)的不定積分，即

因而不定積分可以表示f(x)的任意一個原函數。

直接利用積分公式求出不定積分。

換元積分法可分為第一類換元法與第二類換元法。

一、第一類換元法（即湊微分法）

通過湊微分，最後依託於某個積分公式。進而求得原不定積分。例如二、註：第二類換元法的變換式必須可逆，並且在相應區間上是單調的。

第二類換元法經常用於消去被積函數中的根式。當被積函數是次數很高的二項式的時候，為了避免繁瑣的展開式，有時也可以使用第二類換元法求解。常用的換元手段有兩種：

1、根式代換法，

2、三角代換法。

在實際應用中，代換法最常見的是鏈式法則，而往往用此代替前面所說的換元。

鏈式法則是一種最有效的微分方法，自然也是最有效的積分方法，下面介紹鏈式法則在積分中的應用：

鏈式法則：

我們在寫這個公式時，常常習慣用u來代替g，即：

如果換一種寫法，就是讓：

就可得：

這樣就可以直接將dx消掉，走了一個捷徑。

設函數和u，v具有連續導數，則。移項得到兩邊積分，得分部積分公式

稱公式⑴為分部積分公式．如果積分∫vdu易於求出，則左端積分式隨之得到．

分部積分公式運用成敗的關鍵是恰當地選擇u,v

一般來說，u,v 選取的原則是：

1、積分容易者選為v， 2、求導簡單者選為u。

例子：中應設

分部積分法的實質是：將所求積分化為兩個積分之差，積分容易者先積分。實際上是兩次積分。

有理函數分為整式（即多項式）和分式（即兩個多項式的商），分式分為真分式和假分式，而假分式經過多項式除法可以轉化成一個整式和一個真分式的和．可見問題轉化為計算真分式的積分．

可以證明，任何真分式總能分解為部分分式之和。

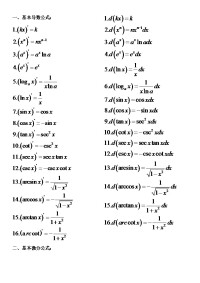
雖然很多函數都可通過如上的各種手段計算其不定積分，但這並不意味著所有的函數的原函數都可以表示成初等函數的有限次複合，原函數不可以表示成初等函數的有限次複合的函數稱為不可積函數。利用微分代數中的微分Galois理論可以證明，如這樣的函數是不可積的。

含有三角函數的積分

例1 求

解：原式=

例2 求

解：原式=