數值孔徑

數值孔徑是透鏡和聚光鏡的主要技術參數，是判斷兩者（尤其對物鏡而言）性能高低（即消位置色差的能力，蔡司公司的數值孔徑是代表消位置色差和倍率色差的能力）的重要標誌。其數值的大小，分別標刻在物鏡和聚光鏡的外殼上。

數值孔徑（NA）是透鏡與被檢物體之間介質的折射率（n）和孔徑角（2α）半數的正弦之乘積。用公式表示如下：NA = n * sin α。孔徑角又稱“鏡口角”，是透鏡光軸上的物體點與物鏡前透鏡的有效直徑所形成的角度。孔徑角越大，進入透鏡的光通量就越大，它與透鏡的有效直徑成正比，與焦點的距離成反比。

這裡必須指出，為了充分發揮物鏡數值孔徑的作用，在觀察時，聚光鏡的NA值應等於或略大於物鏡的NA值。

數值孔徑體現了光纖與光源之間的耦合效率。光源與光纖端面間存在空氣隙，入射到光纖端面的光只有一部分能進入光纖，而進入光纖端面內的光也只有部分符合特定條件的光才能在光纖中發生全內反射而傳播。由圖可知，只有從空氣隙到光纖端面以入射角小於 q0入射的光線才能傳播。q0 實際上是個空間角，也就是說如果光從一個限制在2q0 的錐形區域中入射到光纖端面上，則光可被光纖捕捉。qo 越大，即纖芯與包層的折射率之差越小，光纖捕捉光線的能力越強，而參數sinqo 直接反映了這種能力，我們稱為光纖的數值孔徑NA 。

數值孔徑與其它技術參數有著密切的關係，它幾乎決定和影響著其它各項技術參數。它與解析度成正比，與放大率成正比，焦深與數值孔徑的平方成反比，NA值增大，視場寬度與工作距離都會相應地變小。

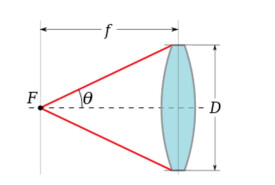
在激光物理領域，數值孔徑的定義略有不同。激光光束在傳播過程中，發生角度很小的發散。在遠離光束最窄點的地方，光束的發散程度與傳播距離大致呈線性關係——相當於光束在“遠場”形成了一個圓錐。在這種情形下，數值孔徑的定義仍然是：

但θ的定義則與之前所述不同。激光光束的並不是一個因受到光闌限制而產生的銳利圓錐，而是一個輻照度隨著離光束中心距離而逐漸降低的高斯光束。針對這種情況，激光物理學家們選擇用光束的發散程度來定義θ，也就是θ由光的傳播方向，以及輻照度降低到波前總輻照度1/e時距光束中軸的距離決定。對於高斯激光束，其數值孔徑與激光最小束斑尺寸有關（其數值孔徑表示激光的發散程度，激光發散程度與激光最小光束直徑有關）：

在多模光纖中，只有沿著特定錐角（也就是所謂受光錐角）進入光纖的光線才能沿著光纖傳播。該錐角的半形即被稱為受光角θmax。對於突變型多模光纖，受光角的大小僅取決於光纖核心與外部包覆層的折射率：

其中，n1是光纖核心的折射率，n2則是包覆層的折射率。儘管更高角度的光也能進入核心層，但這些光是無法在兩層之間的界面上發生全反射的，因而也無法通過光纖傳播。

在顯微鏡系統中，對於給定的物鏡，孔徑角已經固定，若想增大其NA值，唯一的辦法是增大介質折射率n值。基於這一原理，就產生了水浸系物鏡和油浸物鏡。

因介質的折射率n值大於1，NA值就可能大於1。

數值孔徑最大值為1.4，這個數值在理論上和技術上都達到了極限。如果用折射率高的溴萘作介質，溴萘的折射率為1.66,所以NA值可大於1.4。