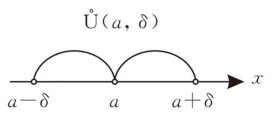
去心鄰域
高數中在a鄰域去掉a數的集合
去心鄰域即在a的鄰域中去掉a的數的集合,應用於高等數學。在拓撲學中,設A是拓撲空間(X,τ)的一個子集,點x∈A。如果存在集合U,滿足U是開集,即U∈τ;點x∈U;U是A的子集,則稱點x是A的一個內點,並稱A是點x的一個鄰域。
只考慮點a鄰近的點,不考慮點a,即考慮點集,稱這個點集為點a的去心鄰域,記為,即。如下圖所示。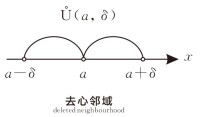

去心鄰域
高等數學中,我們經常會用到一種特殊的開區間,稱這個開區間為點a的鄰域(neighbourhood),記為,即,並稱點a為鄰域的中心,δ為鄰域的半徑。通常δ是較小的實數,所以,a的δ鄰域表示的是a的鄰近的點,如下圖所示。
● 以a為中心的任何開區間都稱為點a的鄰域,記作。
● 設δ是任一正數,則開區間就是點a的一個鄰域,這個鄰域稱為點a的δ鄰域。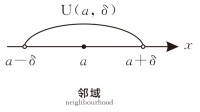

去心鄰域
設A是拓撲空間的一個子集,點。如果存在集合U,滿足
● ● U是開集,即;
● ● 點;
● ● U是A的子集,
則稱點x是A的一個內點,並稱A是點x的一個鄰域。若A是開(閉)集,則稱為開(閉)鄰域。
若非空集合X的子集A是A內所有元素的鄰域,則A為開集。