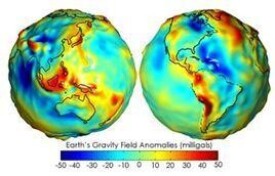
大地測量學
大地測量學
大地測量學,又稱為測地學。根據德國著名大地測量學家F.R. Helmert的經典定義,大地測量學是一門量測和描繪地球表面的科學。也就是研究和測定地球形狀、大小和地球重力場,以及測定地面點幾何位置的學科。它也包括確定地球重力場和海底地形,是測繪學的一個分支。英文解釋:A subdivision of geophysics which includes determination of the size and shape of the earth, the earth`s gravitational field, and the location of points fixed to the earth`s crust in an earth-referred coordinate system. (Source: MGH)"
大地測量學是測繪學的一個分支。研究和測定地球形狀、大小和地球重力場,以及測定地面點幾何位置的學科。
大地測量學中測定地球的大小,是指測定地球橢球的大小;研究地球形狀,是指研究大地水準面的形狀;測定地面點的幾何位置,是指測定以地球橢球面為參考的地面點的位置。將地面點沿法線方向投影於地球橢球面上,用投影點在橢球面上的大地緯度和大地經度表示該點的水平位置,用地面點至投影點的法線距離表示該點的大地高程。這點的幾何位置也可以用一個以地球質心為原點的空間直角坐標系中的三維坐標來表示。
大地測量工作是為大規模測制地形圖提供地面的水平位置控制網和高程式控制制網,為用重力勘探地下礦藏提供重力控制點,同時也為發射人造地球衛星、導彈和各種航天器提供地面站的精確坐標和地球重力場資料。
它的基本任務是研究全球,建立與時相依的地球參考坐標框架,研究地球形狀及其外部重力場的理論與方法,研究描述極移固體潮及地殼運動等地球動力學問題,研究高精度定位理論與方法。

測地學
建立和維持具有高科技水平的國家和全球的天文大地水平控制網和精密水準網以及海洋大地控制網,以滿足國民經濟和國防建設的需要。
研究為獲得高精度測量成果的儀器和方法等。
研究地球表面向橢球面或平面的投影數學變換及有關的大地測量計算。
研究大規模、高精度和多類別的地面網、空間網及其聯合網的數學處理的理論和方法,測量資料庫建立及應用等。
• 幾何大地測量學亦即天文大地測量學:它的基本任務是確定地球的形狀和大小及確定地面點的幾何位置。
• 物理大地測量學也稱理論大地測量學:它的基本任務是用物理方法(重力測量)確定地球形狀及其外部重力場。
• 空間大地測量學:主要研究人造地球衛星及其他空間探測器為代表的空間大地測量的理論,技術與方法。
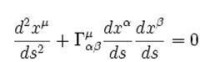
測地方程
17世紀以前,大地測量學處於萌芽狀態。公元前3世紀,埃拉托色尼首先應用幾何學中圓周上一段弧的長度、對應的中心角同圓半徑的關係,計算地球的半徑長度。公元724年,中國唐代的南宮說等人在張遂(一行)的指導下,首次在今河南省境內實測一條長約300千米的子午弧。其他國家也進行過類似的工作。但當時測量工具簡陋,技術粗糙,所得結果精度不高,只是測量地球大小的嘗試。
1687年I.牛頓發表萬有引力定律之後,1690年荷蘭c.惠更斯在其著作《論重力起因》中,根據地球表面的重力值從赤道向兩極增加的規律,得出地球的外形為兩極略扁的扁球體論斷。1743年法國A.一C.克菜羅發表《地球形狀理論》,進一步給出由重力數據和地球自轉角速度確定地球扁率的克萊羅定理。此外,17世紀初,荷蘭的w.斯涅耳首創三角測量。隨後望遠鏡、測微器、水準器等發明,測量儀器精度大幅度提高,為大地測量學的發展奠定技術基礎。17世紀末,大地測量學形成至衛星大地測量的出現,這一階段的大地測量學通常稱為經典大地測量學。主要標誌是以地面測角、測距、水準測量和重力測量為技術手段解決陸地區域性大地測量問題。弧度測量、三角測量、幾何高程測量以及橢球面大地測量理論的發展,形成幾何大地測量學;建立了重力場的位理論並發展了地面重力測量,形成物理大地測量學。
1683~1718年,法國卡西尼父子(G.D.Cassini和J.Cassini)在通過巴黎的子午圈上用三角測量法測量弧幅達8°20’的弧長,推算出地球橢球的長半軸和扁率。由於天文緯度觀測沒有達到必要的精度,加之兩個弧段相近,以致得出了負的扁率值,即地球形狀是兩極伸長的橢球,與惠更斯根據力學定律作出的推斷正好相反。為了解決這一疑問,法國科學院於1735年派遣兩個測量隊分別赴高緯度地區拉普蘭(位於瑞典和芬蘭的邊界上)和近赤道地區秘魯進行子午弧度測量,全部工作於1744年結束。兩處的測量結果證實緯度愈高,每度子午弧愈長,即地球形狀是兩極略扁的橢球。至此,關於地球形狀的物理學論斷得到了弧度測量結果的有力支持。
另一個著名的弧度測量是J.B.J.德朗布爾於1792~1798年間進行的弧幅達9°40’的法國子午弧的測量。由這個新子午弧和1735~1744年間測量的秘魯子午弧的數據,推算了子午圈一象限的弧長,取其千萬分之一作為長度單位,命名為一米。這是米制的起源。
從18世紀起,繼法國之後,一些歐洲國家也都先後開展了弧度測量工作,並把布設方式由沿子午線方向發展為縱橫交叉的三角鎖或三角網。這種工作不再稱為弧度測量,而稱為天文大地測量。中國清代康熙年間(1708~1718)為編製《皇輿全覽圖》,曾實施大規模的天文大地測量。在這次測量中,也證實高緯度的每度子午弧比低緯度的每度子午弧長。另外,清代康熙皇帝還決定以每度子午弧長為200里來確定里的長度。
19世紀起,許多國家都開展全國天文大地測量工作,其目的並不僅是為求定地球橢球的大小,更主要的是為測制全國地形圖提供大量地面點的精確幾何位置。這就推動了幾何大地測量的發展。
①為了檢校天文大地測量的大量觀測數據,求出最可靠的結果和評定觀測精度,法國A.一M.勒讓德於1806年首次發表最小二乘法的理論。事實上,德國數學家和大地測量學家C.F.高斯在1794年已經應用這一理論推算小行星的軌道,此後又用最小二乘法處理天文大地測量成果,把它發展到相當完善的程度,形成測量平差法,至今仍廣泛應用於大地測量。
②橢球面上三角形的解算和大地坐標的推算,高斯於1828年在其著作《曲面通論》中提出橢球面三角形的解法。關於大地坐標的推算,許多學者提出了多種公式,高斯於1822年發表橢球面投影到平面上的正形投影法,這是大地坐標換算成平面坐標的最佳方法,至今仍在廣泛應用。
③利用天文學大地測量成果推算地球橢球長半軸和扁率,德國F.R.赫爾墨特提出在天文大地網中所有天文點的垂線偏差平方和為最小的條件下,解算與區域大地水準面最佳擬合的橢球參數及其在地球體中定位的方法。以後這一方法被稱為面積法。
自1743年克萊羅發表了《地球形狀理論》之後,物理大地測量的最重要發展是1849年英國的G.G.斯托克斯提出的斯托克斯定理。根據這一定理,可以利用地面重力測量結果研究大地水準面形狀。但它要求首先將地面重力測量結果歸算到大地水準面上,由於地殼密度未知,這種歸算不能嚴格實現。儘管如此,斯托克斯定理還是推動了大地水準面形狀的研究工作。大約100年後,蘇聯的M.S.莫洛堅斯基於1945年提出莫洛堅斯基理論,它不需任何歸算,便可以直接利用地面重力測量數據嚴格地求定地面點到參考橢球面的距離(大地高程)。它避開了理論上無法嚴格求定的大地水準面,直接求定地面點的大地高程。利用這種高程,可把大地測量的地面觀測值準確地歸算到橢球面上,使天文大地測量的成果處理不因歸算不準確而帶來誤差。伴隨著莫洛堅斯基理論產生的天文重力水準測量方法和正常高系統已被許多國家採用。這是在衛星重力測量技術出現以前,由地面重力測量研究地球形狀和確定地球重力場的理論和方法,稱為經典物理大地測量。
經典大地測量由於其主要測量技術手段(測角和測邊)和方法本身的局限性,測量精度已近極限,測量範圍也難於達到佔地球面積70%的海洋和陸地自然條件惡劣的地區(高原、沙漠和原始森林等)。1957年第一顆人造地球衛星發射成功后,利用人造衛星進行大地測量成為主要技術手段,從此發展到現代大地測量。其標誌是產生衛星大地測量,突破了米級測量精度,從區域性相對大地測量發展到全球的大地測量,從測量靜態地球發展到可測量地球的動力學效應。
1966年美國的W.M.考拉發表《衛星大地測量理論》一書,為衛星大地測量的發展奠定基礎。同時,對衛星跟蹤觀測定軌技術得到迅速發展,從照相觀測發展到衛星激光測距(8LR)和衛星多普勒觀測。20世紀70年代美國首先建立衛星多普勒導航定位系統,根據精密測定的衛星軌道根數,能夠以土1米或更高的精度測定任一地面點在全球大地坐標系中的地心坐標;90年代美國又發展了新一代導航定位系統,即全球定位系統(GPS),以其廉價、方便、全天候的優勢迅速在全球普及,成為大地測量定位的常規技術。俄羅斯發展了全球導航衛星系統(GLONASS),歐洲正在啟動伽利略全球衛星導航定位系統(Galileo)。衛星大地測量不僅廣泛用於高精度測定地面點的位置,還用於確定全球重力場,並形成一門新的大地測量分支,即衛星重力學。
衛星激光測距對衛星的跟蹤測量可以精確測定衛星軌道的攝動,當分離出占攝動主要部分的地球引力攝動,由此推算地球引力位球諧展開的低階位係數。20世紀70年代開始衛星雷達測高,后又研製和發展了多代衛星測高系統,用於精確測定平均海面的大地高,確定海洋大地水準面,並反求海洋重力異常,解析度優於lO千米,精度優於分米級。
SLR和甚長基線干涉測量(VLBI),可以厘米級或更優的精度監測板塊的運動速率、極移和地球自轉速率的變化。GPS更能以毫米級精度測定板塊內地塊的相對運動及地殼形變,還廣泛用於監測斷層和地震活動、極地冰原和陸地冰川的運動和變化以及冰后回彈現象。
衛星測高已成為確定高解析度全球海洋大地水準面的最廉價有效的手段,GPS也成為海洋導航定位的主要工具,定位精度比傳統的天文導航和無線電導航精度提高1~2個數量級,多波束聲吶測深相對精度已達到或接近111000。海底大地控制網和海底地形測量的規模和精度在不斷提高。
大地測量學從形成到現在已有 300多年的歷史,雖然在研究地球形狀、地球重力場和測定地面點幾何位置各方面都已取得了可觀的成就,但從整體來看,仍存在著若干不足之處,有待於今後繼續研究解決。
①衛星大地測量已經全面地和均勻地求出了地球重力場(包括大地水準面)的總貌,但還不能求得其精細結構。這是由於衛星運行的軌道至少在地面上方 200公里以上,對地球重力場效應的分辨能力也只能達到這一數量級。目前地面重力測量在全球的分佈極不均勻,有待繼續擴展。在海洋上空利用衛星雷達測高技術測定海洋大地水準面的起伏已取得了較好的結果。由天文大地測量求得的垂線偏差和由天文重力水準所得的大地水準面起伏,也都是地球重力場的信息。所以要研究地球重力場全面而精細的結構,必須綜合利用衛星、物理和幾何大地測量的各種信息,進行統一的處理,有人稱之為整體大地測量。這是研究地球重力場的發展趨勢。
②18世紀以來進行的天文大地測量,各國大都採用不同的參考橢球,建立獨立的坐標系。20世紀以來,通過聯測和改算,有些獨立坐標系連成一體,形成了西歐、北美、蘇聯和東歐、印度、中國、澳大利亞等若干個較大的坐標系。直到全球衛星大地測量開展以後,特別是由於衛星多普勒定位技術的發展,才使建立全球統一的地心坐標系成為可能。許多國家都在原有的天文大地網內加測衛星多普勒定位點,把天文大地網和衛星定位網結合起來。這已成為當前的趨勢。正在發展中的衛星射電干涉測量技術,不但有可能加強天文大地網,甚至可能局部代替傳統的天文大地網。可以預期,測定地面點幾何位置的大地網的布設和加密,將來必然向綜合利用各種技術的方向發展;而如何最有效地和最經濟地綜合利用各種技術,也必然是今後的研究課題。
③海洋研究和海洋資源開發是當前受到重視的課題,但海洋大地測量目前尚處於初級發展階段。近年來聲吶技術發展很快,已成為在海水中進行測量的重要手段。如何利用這種技術進行海洋大地測量,也是今後的研究方向。
④全球只有為數很少的一些固定站在進行甚長基線干涉測量工作。為了更好地研究地殼構造運動,還必須發展流動站,測量較短的基線。同時還要再利用固體潮觀測、衛星激光測距和衛星射電干涉測量等技術,綜合全部測量結果,將為探索地震預報提供寶貴的信息。